1206. Stacking Cylinders & 1012. Stacking Cylinders

TAG 简单几何计算

 

这两道题题目是一样的，不过输出格式有点不同，而且1206的Sample input故意设下陷阱：让人误以为输入数据有序。

我之前没有排序，wa了。(╬▔ ω▔)

 

圆形的位置不好处理，我们可以考虑圆心，变成三角形来分析。

题目说明只有相邻层会接触。所以问题变得比较简单，而且我们可以逐层计算上去，最终得到答案。

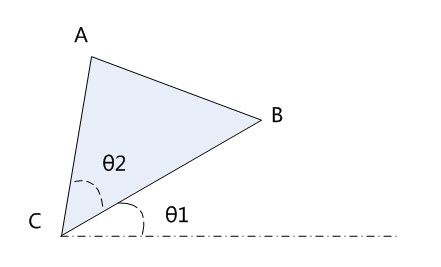
连接相邻的2个圆心和对应上方的圆心，显然AC=AB=2，再算 θ1 和 θ2 两个角便能得出答案。C 和 B 的坐标在递推时已求出，显然 θ1 和 θ2很容易算。当然，这里画的三角形是“左倾”的，还有“右倾”的情况，所以注意算 θ1 的时候，在求边时不要用绝对值，这样 θ1 可正可负，最后直接和 θ2 相加即可。

三角函数、细节的处理看1206的代码

#include <stdio.h> #include <math.h> #include <algorithm> using namespace std; struct node { double x,y; bool operator<(const node &b)const { return x<b.x; } }; node a[10][10]; int t,n; int casenum; double abs(double x) { return x<0.0? -x: x; } void cal_pos(int i, int j) { double ang1, ang2; ang1= (a[i-1][j+1].y-a[i-1][j].y)/(a[i-1][j+1].x-a[i-1][j].x); ang1=atan(ang1); ang2=sqrt( pow( (a[i-1][j].y-a[i-1][j+1].y),2.0 ) +pow( (a[i-1][j+1].x-a[i-1][j].x),2.0 ) ); ang2=acos(ang2/4.0); a[i][j].x=a[i-1][j].x+2*cos(ang1+ang2); a[i][j].y=a[i-1][j].y+2*sin(ang1+ang2); } int main(int argc, char *argv[]) { scanf("%d", &t); casenum=0; while ( t-- ) { ++casenum; scanf("%d", &n); for (int i=0; i<n; ++i) { scanf("%lf", &a[0][i].x); a[0][i].y=1.0; } sort(&a[0][0], &a[0][0]+n); for (int i=1; i<n; ++i) { for (int j=0; j<n-i; ++j) { cal_pos(i,j); } } printf("%d: %.4lf %.4lf/n",casenum, a[n-1][0].x, a[n-1][0].y ); } return 0; }