第八周实验报告任务1 实现复数类中的运算符重载
/* (程序头部注释开始)
* 程序的版权和版本声明部分
* Copyright (c) 2011, 烟台大学计算机学院学生
* All rights reserved.
* 文件名称:定义一个复数类重载运算符+、-、*、/,使之能用于复数的加减乘除。
* 作 者: 陶锋
* 完成日期: 2012 年 04 月 09 日
* 版 本 号: V1.0
* 对任务及求解方法的描述部分
* 输入描述:
* 问题描述:
* 程序输出:
* 程序头部的注释结束
*/
方案一:用类的成员函数完成运算符的重载:
#include <iostream>
using namespace std;
class Complex
{
public:
Complex(){real=0;imag=0;}
Complex(double r,double i){real=r;imag=i;}
Complex operator+(Complex &c2);
Complex operator-(Complex &c2);
Complex operator*(Complex &c2);
Complex operator/(Complex &c2);
void display();
private:
double real;
double imag;
};
//下面定义成员函数
Complex Complex::operator+(Complex &c2)
{
Complex c;
c.real=real+c2.real;
c.imag=imag+c2.imag;
return c;
}
Complex Complex::operator-(Complex &c2)
{
Complex c;
c.real=real-c2.real;
c.imag=imag-c2.imag;
return c;
}
Complex Complex::operator*(Complex &c2)
{
Complex c;
c.real=real*c2.real-imag*c2.imag;
c.imag=imag*c2.real+real*c2.imag;
return c;
}
Complex Complex::operator/(Complex &c2)
{
Complex c;
c.real=(real*c2.real+imag*c2.imag)/(c2.real*c2.real+c2.imag*c2.imag);
c.imag=(imag*c2.real-real*c2.imag)/(c2.real*c2.real+c2.imag*c2.imag);
return c;
}
void Complex::display()
{
cout<<"("<<real<<","<<imag<<"i)"<<endl;
}
int main()
{
Complex c1(3,4),c2(5,-10),c3;
cout<<"c1=";
c1.display();
cout<<"c2=";
c2.display();
c3=c1+c2;
cout<<"c1+c2=";
c3.display();
c3=c1-c2;
cout<<"c1-c2=";
c3.display();
c3=c1*c2;
cout<<"c1*c2=";
c3.display();
c3=c1/c2;
cout<<"c1/c2=";
c3.display();
system("pause");
return 0;
}
方案二:请用类的友元函数,而不是成员函数,完成上面提及的运算符的重载:
#include<iostream> using namespace std; class Complex { public: Complex(){real=0;imag=0;} Complex(double r,double i){real=r;imag=i;} friend Complex operator+(Complex &c1,Complex &c2); friend Complex operator-(Complex &c1,Complex &c2); friend Complex operator*(Complex &c1,Complex &c2); friend Complex operator/(Complex &c1,Complex &c2); friend void display(Complex &c2); private: double real; double imag; }; //下面定义友元函数
//复数相加: (a+bi)+(c+di)=(a+c)+(b+d)i. Complex operator+(Complex &c1,Complex &c2) { Complex c; c.real=c1.real+c2.real; c.imag=c1.imag+c2.imag; return c; } //复数相减:(a+bi)-(c+di)=(a-c)+(b-d)i. Complex operator-(Complex &c1,Complex &c2) { Complex c; c.real=c1.real-c2.real; c.imag=c1.imag-c2.imag; return c; } //复数相乘:(a+bi)(c+di)=(ac-bd)+(bc+ad)i. Complex operator*(Complex &c1,Complex &c2) { Complex c; c.real=c1.real*c2.real-c1.imag*c2.imag; c.imag=c1.imag*c2.real+c1.real*c2.imag; return c; } //复数相除:(a+bi)/(c+di)=(ac+bd)/(c^2+d^2) +(bc-ad)/(c^2+d^2)i Complex operator/(Complex &c1,Complex &c2) { Complex c; double d=c2.real*c2.real+c2.imag*c2.imag; c.real=(c1.real*c2.real+c1.imag*c2.imag)/d; //此处有危险未排除:除法溢出 c.imag=(c1.imag*c2.real-c1.real*c2.imag)/d; return c; } void display(Complex &c2) { cout<<"("<<c2.real<<","<<c2.imag<<"i)"<<endl; }
int main() { Complex c1(3,4),c2(5,-10),c3; cout<<"c1="; display(c1); cout<<"c2="; display(c2); c3=c1+c2; cout<<"c1+c2="; display(c3); c3=c1-c2; cout<<"c1-c2="; display(c3); c3=c1*c2; cout<<"c1*c2="; display(c3); c3=c1/c2; cout<<"c1/c2="; display(c3); system("pause"); return 0; }
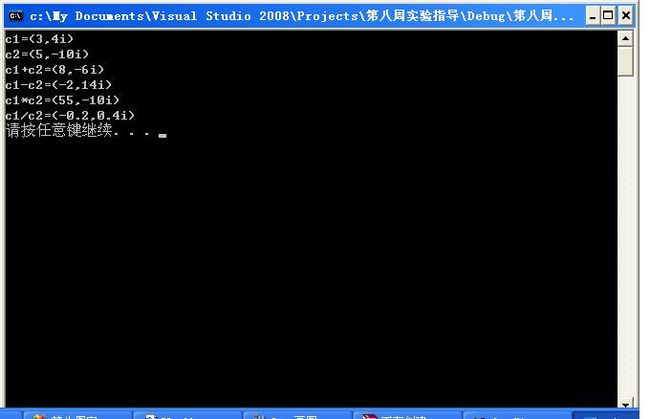
运行结果:
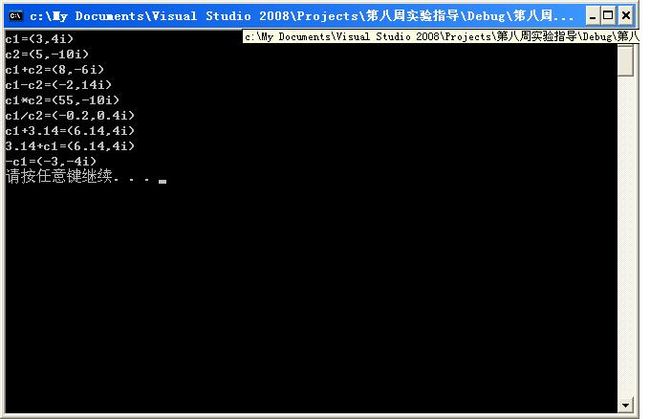
方案三:在方案二的基础上,扩展+、-、*、/运算符的功能,使之能与double型数据进行运算。设Complex c; double d; c?d和d?c的结果为将d视为实部为d的复数同c运算的结果(其中?为+、-、*、/之一)。另外,定义一目运算符-,-c相当于0-c。
#include<iostream>
using namespace std;
class Complex
{
public:
Complex(){real=0;imag=0;}
Complex(double r,double i){real=r;imag=i;}
friend Complex operator+(Complex &c1,Complex &c2);
friend Complex operator-(Complex &c1,Complex &c2);
friend Complex operator-(Complex &c2);
friend Complex operator*(Complex &c1,Complex &c2);
friend Complex operator/(Complex &c1,Complex &c2);
friend Complex operator+(Complex &c1,const double &d);
friend Complex operator+(const double &d, Complex &c);
friend void display(Complex &c2);
private:
double real;
double imag;
};
//下面定义友元函数
//复数相加: (a+bi)+(c+di)=(a+c)+(b+d)i.
Complex operator+(Complex &c1,Complex &c2)
{
Complex c;
c.real=c1.real+c2.real;
c.imag=c1.imag+c2.imag;
return c;
}
Complex operator+(Complex &c1,const double &d)
{
return Complex(c1.real+d, c1.imag);
}
Complex operator+(const double &d, Complex &c1)
{
return Complex(c1.real+d, c1.imag);
}
//复数相减:(a+bi)-(c+di)=(a-c)+(b-d)i.
Complex operator-(Complex &c1,Complex &c2)
{
Complex c;
c.real=c1.real-c2.real;
c.imag=c1.imag-c2.imag;
return c;
}
Complex operator-(Complex &c2)
{
return Complex(-c2.real, -c2.imag);
}
//复数相乘:(a+bi)(c+di)=(ac-bd)+(bc+ad)i.
Complex operator*(Complex &c1,Complex &c2)
{
Complex c;
c.real=c1.real*c2.real-c1.imag*c2.imag;
c.imag=c1.imag*c2.real+c1.real*c2.imag;
return c;
}
//复数相除:(a+bi)/(c+di)=(ac+bd)/(c^2+d^2) +(bc-ad)/(c^2+d^2)i
Complex operator/(Complex &c1,Complex &c2)
{
Complex c;
double d=c2.real*c2.real+c2.imag*c2.imag;
c.real=(c1.real*c2.real+c1.imag*c2.imag)/d; //此处有危险未排除:除法溢出
c.imag=(c1.imag*c2.real-c1.real*c2.imag)/d;
return c;
}
void display(Complex &c2)
{
cout<<"("<<c2.real<<","<<c2.imag<<"i)"<<endl;
}
int main()
{
Complex c1(3,4),c2(5,-10),c3,c4;
cout<<"c1=";
display(c1);
cout<<"c2=";
display(c2);
c3=c1+c2;
cout<<"c1+c2=";
display(c3);
c3=c1-c2;
cout<<"c1-c2=";
display(c3);
c3=c1*c2;
cout<<"c1*c2=";
display(c3);
c3=c1/c2;
cout<<"c1/c2=";
display(c3);
c4=c1+3.14;
cout<<"c1+3.14=";
display(c4);
c4=3.14+c1;
cout<<"3.14+c1=";
display(c4);
c4=-c1;
cout<<"-c1=";
display(c4);
system("pause");
return 0;
}
感悟:利用成员函数,友元函数,和运算符的不同方式来实现的这个函数能体会得到各自的好处