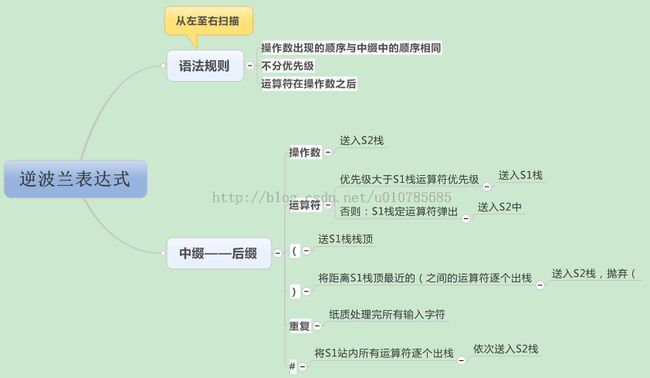
波兰、逆波兰表达式
软考习题里遇到了这样一道题,给出了一个逆波兰式,让求它对应的中缀表达式。
逆波兰式:ab-cd+* ,它的中缀表达式是(a-b)*(c+d)
思考:
这让我蒙圈了,这是为什么呢。怎么得到的呢,应该有什么规律的吧。
首先我们要知道:
波兰式:前缀表达式
逆波兰式:后缀表达式
了解这三个表达式之前,我们需要知道
| 表达式 |
解释 |
例子 |
| 前缀 |
不含括号的的算数表达式,将运算符写在前面,操作数写在后面 |
*+ 2 1 3 |
| 中缀 |
必须含括号,操作符处于操作数的中间 |
(2+1)*3 |
| 后缀 |
不含括号,运算符放在两个运算对象的后面。 |
3 2 + 3 * |
这三个表达式的重点就是他们之间的转换,学会转换,对这三个表达式也就了解的差不多了,那么到底怎么转换的呢?
给出一个中缀表达式,转化为前缀和后缀表达式。
例如我们做的这道题,中缀表达式答案是(a-b)*(c+d),我们看来验证一下他正确不。
步骤:
第一步:按照运算符的优先级,对所有的运算单位加括号。
((a-b)*(c+d))
第二步转换:
转换为前缀:把运算符号移动到对应的括号前面,然后去掉括号。
“*”移最前面;“-”移到 -(ab);“+”移到+(cd)
得到:*-(ab)+(cd)去括号后:*-ab+cd
转换为后缀:
“*”移到最后;“-”移到(ab)-;“+”移到(cd)+
得到:(ab)-(cd)+*去括号后:ab-cd+*
以上方法适用于较为简单的选择题,对于真正的算法题我觉得就给多想想了。
对于前缀、中缀和后缀的知识不仅是是他们的转化,还有很多知识,以后会再了解的。
而对于逆波兰式,冲着这么好听的名字,也得明白他是什么吧,其实就是波兰逻辑学家的一个人发明的一种表示表达式的方式。这种表示法的优点就是根据运算对象和算符的出现次序进行计算,便于用栈实现求值。
只学会了简单的转换,对于这方面的认识还远远不够,其实中缀表达式转化为后缀表达式也是数据结构里的一个算法题。逆波兰表达式只用于两种简单操作,入栈和出栈。按顺序扫描逆波兰表达式,如果当前字符是变量或者数字就压栈,如果是运算符,则将栈顶两个元素弹出想想运算,结果再入栈,最后当表达式扫描完后,栈里就是结果。
个人理解的不是很深刻,具体到算法题估计还是有一定的困难,不过走一步算一步,能理解多少是多少。这个算法会不会考也不知道,不总结就更不认识了。先总结了再说,有什么错误请大家指点,互相交流。