后缀数组 学习笔记

一、几种数组：
    1、suffix(i)  字符串 s的从 第 i个字符开始的后缀表示为 suffix(i)

    2、后缀数组 SA：它保存 1..n的某个排列 SA[1 ] ，SA[2] ， …… ， SA[n] ，并且保证suffix(SA[i]) <Suffix(SA[i+1]) ， 1 ≤ i<n 。也就是将 S的 n 个后缀从小到大进行排序之后把排好序的后缀的开头位置顺次放入 SA 中。就是说排名第i的后缀首字母在字符串s的下标为sa[i]。

3、名次数组 Rank[i]：保存的是 Suffix(i)在所有后缀中从小到大排列的 “ 名次 ” 。就是说 在字符串s中下标为i的字符， 以该字符开始的后缀Suffix(i)是第Rank[i]大的后缀。若 sa[i]=j，则 rank[j]=i。后缀数组sa与名次数组rank的关系为互逆关系。

4、height数组：定义height[i]=suffix(sa[i-1])和suffix(sa[i]) 的最长公共前缀，也就是排名相邻的两个后缀的最长公共前缀。

 

二、算法步骤：

 

倍增算法

一、主要思路：倍增，s[i..i + 2k − 1]的排名通过s[i..i + 2k − 1 − 1]和s[i + 2k − 1..i + 2k −1]的排名得到。

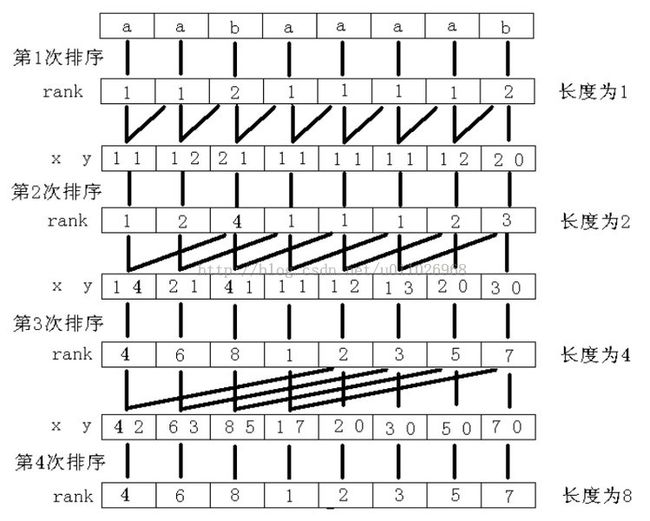
二、简要过程：已知每个长度为2k −1的字符串的排名，则可作为每个长度为2k的字符串求排名的关键字xy，s[i..i+ 2k − 1]第一关键字x为s[i..i +2k − 1 − 1]的排名，第二关键字y为s[i +2k − 1..i + 2k −1]的排名。以字符串aabaaaab为例：

1. k=0,对每个字符开始的长度为20 = 1的子串进行排序，得到rank[1..8]={1,1,2,1,1,1,1,2}

2. k=1,对每个字符开始的长度为21 = 2的子串进行排序：由k=0的rank得关键字xy[1..8]={11,12,21,11,11,11,12,20}，得到rank[1..8]={1,2,4,1,1,1,2,3}

3. k=2,对每个字符开始的长度为22 = 4的子串进行排序：由k=1的rank得关键字xy[1..8]={14,21,41,11,12,13,20,30}，得到rank[1..8]={4,6,8,1,2,3,5,7}

4. k=3,对每个字符开始的长度为23 = 8的子串进行排序：由k=2的rank得关键字xy[1..8]={42,63,85,17,20,30,50,70}，得到rank[1..8]={4,6,8,1,2,3,5,7}

注意：在排序过程中，rank[]可以有相同排名，但是sa[]排第几是没有相同的（就像Excel的排序，sa相当于编号，rank相当于排名）。这点可以从程序中体现。建议读者跟踪一下程序体会一下。

整个过程如图：

注意上图中由k/2到k 先比k/2时的rank[i] rank[j],再比rank[i+k/2] rank[js+k/2]

从而得到长度为k的rank，由rank排序的到sa

由height数组可得，对于j和k ，不妨设rank[j]<rank[k],则有以下性质：suffix(j) 和 suffix(k) 的最长公共前缀为height[rank[j]+1],height[rank[j]+2], height[rank[j]+3], …,height[rank[k]] 中的最小值。

void sorting(int j)//基数排序
 {
 	memset(sum,0,sizeof(sum));
 	for (int i=1; i<=s.size(); i++) sum[ rank[i+j] ]++;
 	for (int i=1; i<=maxlen; i++) sum[i]+=sum[i-1];
 	for (int i=s.size(); i>0; i--)
             tsa[ sum[ rank[i+j] ]-- ]=i;
        //对第二关键字计数排序，tsa代替sa为排名为i的后缀是tsa[i] 
 
 	memset(sum,0,sizeof(sum));
 	for (int i=1; i<=s.size(); i++) sum[ rank[i] ]++;
 	for (int i=1; i<=maxlen; i++) sum[i]+=sum[i-1];
 	for (int i=s.size(); i>0; i--)
             sa[ sum[ rank[ tsa[i] ] ]-- ]= tsa[i]; 
        //对第一关键字计数排序,构造互逆关系 
 }
 
 void get_sa()
 {
 	int p;
 	for (int i=0; i<s.size(); i++) trank[i+1]=s[i];
 	for (int i=1; i<=s.size(); i++) sum[ trank[i] ]++;
 	for (int i=1; i<=maxlen; i++) sum[i]+=sum[i-1];
 	for (int i=s.size(); i>0; i--) 
 		sa[ sum[ trank[i] ]-- ]=i;
 	rank[ sa[1] ]=1;
 	for (int i=2,p=1; i<=s.size(); i++)
 	{
 		if (trank[ sa[i] ]!=trank[ sa[i-1] ]) p++;
 		rank[ sa[i] ]=p;
 	}//第一次的sa与rank构造完成
 	for (int j=1; j<=s.size(); j*=2)
 	{
 		sorting(j);
 		trank[ sa[1] ]=1; p=1; //用trank代替rank 
 		for (int i=2; i<=s.size(); i++)
 		{
 			if ((rank[ sa[i] ]!=rank[ sa[i-1] ]) || (rank[ sa[i]+j ]!=rank[ sa[i-1]+j ])) p++;
 			trank[ sa[i] ]=p;//空间要开大一点，至少2倍
 		}
 		for (int i=1; i<=s.size(); i++) rank[i]=trank[i];
 	}
 }

//吉林大学模板
#define N 1001

char s[N];  // N > 256
int n, sa[N], height[N], rank[N], tmp[N], top[N];
void makesa(){  // O(N * log N)
    int i, j, len, na;
    na = (n < 256 ? 256 : n);
    memset(top, 0, na * sizeof(int));
    for(i = 0; i < n ; i++) top[ rank[i] = s[i] & 0xff ]++;
    for(i = 1; i < na; i++) top[i] += top[i - 1];
    for(i = 0; i < n ; i++) sa[ --top[ rank[i] ] ] = i;
    for(len = 1; len < n; len <<= 1) {
        for(i = 0; i < n; i++) {
            j = sa[i] - len; if(j < 0) j += n;
            tmp[ top[ rank[j] ]++ ] = j;
        }
        sa[ tmp[ top[0] = 0 ] ] = j = 0;
        for(i = 1; i < n; i++) {
            if(rank[ tmp[i] ] != rank[ tmp[i-1] ] ||
            rank[ tmp[i]+len ]!=rank[ tmp[i-1]+len ])
            top[++j] = i;
            sa[ tmp[i] ] = j;
        }
        memcpy(rank, sa , n * sizeof(int));
        memcpy(sa , tmp, n * sizeof(int));
        if(j >= n - 1) break;
   }
}

void lcp(){  // O(4 * N)
    int i, j, k;
    for(j = rank[height[i=k=0]=0]; i < n - 1; i++, k++)
        while(k >= 0 && s[i] != s[ sa[j-1] + k ])
            height[j] = (k--), j = rank[ sa[j] + 1 ];
}

我个人用的 巫泽俊 的代码模板（注释是我自己写的，有问题的地方请指教）：

/*******************************/
//WZJ P380
//后缀数组+LCP+字符串匹配
//注意:1、此代码中k是全局变量 别乱用
//     2、algorithm
/*******************************/
#define MAXN 1001

int n,k;//n=strlen(s);

int Rank[MAXN];
int tmp[MAXN];

/*使用Rank对sa排序*/
bool cmpSa(int i, int j)
{
    if(Rank[i] != Rank[j])return Rank[i] < Rank[j];
    else
    {   /*下面的Rank[t]，已经是以t开头长度小于等于k/2的，
        sa[i]的名次，只是以i开头的后缀，而长度不同*/
        int ri = i+k <=n? Rank[i+k]:-1;
        int rj = j+k <= n ? Rank[j+k]:-1;
        return ri <rj;
    }
}

/*计算SA*/
void sa(char *s, int *sa)
{
    //n=strlen(s);
    for(int i=0;i<=n;i++){
        sa[i]=i;Rank[i] = i < n?s[i]:-1;
    }

    /*利用长度为k的字符串对长度为2*k的字符串排序*/
    for(k=1;k<=n;k*=2)/*注意此代码中k是全局变量 别乱用*/
    {
        sort(sa,sa+n+1,cmpSa);
        tmp[sa[0]] = 0;
        for(int i=1;i<=n;i++){
            tmp[sa[i]] = tmp[sa[i-1]] +(cmpSa(sa[i-1],sa[i])?1:0);
            /*这一句很关键，等号右侧的sa[i]在此循环里表示第i大的长度小于等于k/2的字符串，
              从而求出第i大的长度小于等于k的字符串的sa[i]*/
        }
        for(int i=0;i<=n;i++){
            Rank[i] = tmp[i];
        }
    }
}

以上总结来源于：

http://baike.baidu.com/link?url=uDN3KmJYj4Z9rEXlGk_JLk8mqwJa_XSMxGwFq23_9aO0W8a1ajbI6oL4p09SU1DyRRm4syapDMzp3YWZwvyttq

 

http://www.nocow.cn/index.php/%E5%90%8E%E7%BC%80%E6%95%B0%E7%BB%84

 

力荐 ：http://www.cnblogs.com/staginner/archive/2012/02/02/2335600.html

 

以及个人的理解归纳