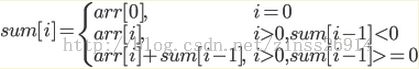最大连续子序列乘积
前言
虽然今天是周六,本来应该写论文开题报告的,无奈实在是项目太工程了,可写东西不多,所以来九度oj做下题目缓解一下心情,最大连续子序列乘积是典型的动态规划题目,据说小米2013年校园招聘笔试考过,这里记录一下
题目
题目描述: 给定一个浮点数序列(可能有正数、0和负数),求出一个最大的连续子序列乘积。 输入: 输入可能包含多个测试样例。 每个测试样例的第一行仅包含正整数 n(n<=100000),表示浮点数序列的个数。 第二行输入n个浮点数用空格分隔。 输入数据保证所有数字乘积在双精度浮点数表示的范围内。 输出: 对应每个测试案例,输出序列中最大的连续子序列乘积,若乘积为浮点数请保留2位小数,如果最大乘积为负数,输出-1。 样例输入: 7 -2.5 4 0 3 0.5 8 -1 5 -3.2 5 -1.6 1 2.5 5 -1.1 2.2 -1.1 3.3 -1.1 样例输出: 12 64 8.78
思路
最大连续子序列乘积和最大连续子序列和不同,这里先回忆一下最大连续子序列和的最优解结构:
最大连续子序列和
我们用sum[i]来表示以arr[i]结尾的最大连续子序列和,则状态转移方程为:
最大连续子序列乘积
考虑存在负数的情况(ps:负负会得正),因此我们用两个辅助数组,max[i]和min[i],max[i]来表示以arr[i]结尾的最大连续子序列乘积,min[i]来表示以arr[i]结尾的最小连续子序列乘积,因此状态转移方程为:
and
有了状态转移方程,dp代码就很容易实现了,看到这里还不理解的同学,我建议你多花点时间用在算法学习上吧!
AC代码
#include <stdio.h>
#include <stdlib.h>
double maxNumInThree(double a, double b, double c)
{
double max;
max = (a > b) ? a : b;
max = (max > c) ? max : c;
return max;
}
double minNumInThree(double a, double b, double c)
{
double min;
min = (a < b) ? a : b;
min = (min < c) ? min : c;
return min;
}
int main(void)
{
int i, n;
double *arr, *max, *min, res;
while (scanf("%d", &n) != EOF) {
arr = (double *)malloc(sizeof(double) * n);
max = (double *)malloc(sizeof(double) * n);
min = (double *)malloc(sizeof(double) * n);
for (i = 0; i < n; i ++)
scanf("%lf", arr + i);
// 动态规划求最大连续子序列乘积
max[0] = min[0] = res = arr[0];
for (i = 1; i < n; i ++) {
max[i] = maxNumInThree(arr[i], max[i - 1] * arr[i], min[i - 1] * arr[i]);
min[i] = minNumInThree(arr[i], max[i - 1] * arr[i], min[i - 1] * arr[i]);
if (max[i] > res)
res = max[i];
}
if (res >= 0) {
// 判断是否为浮点数
if ((res - (int)res) == 0)
printf("%d\n", (int)res);
else
printf("%.2lf\n", res);
} else {
printf("-1\n");
}
free(arr);
}
return 0;
}
/**************************************************************
Problem: 1501
User: wangzhengyi
Language: C
Result: Accepted
Time:110 ms
Memory:4964 kb
****************************************************************/