LISP 学习笔记 (四)-链表,递归和符号
*声明:所有参考资料均出自网络,版权归原作者所有
参考:LISP Tutorial 1: Basic LISP Programming: http://www.cs.sfu.ca/CC/310/pwfong/Lisp/1/tutorial1.html
这次大脑饱和,个人没作太多的思考,文中大部分仅仅翻译了上面指导的部分文字。个人觉得链表和LISP中的递归处理是LISP的精粹所在,权当好好去领悟。水平有限,难免有失误之处。欢迎各位指导和讨论~
用了word进行编辑,全文见下:
链表(Lists)
LISP
不仅支持数值类型的运算,它还支持符号(symbol)类型的运算。LISP中使用链表(list)这种数据结构来支持符号运算。实际上,LISP就是链表处理(LISt Processing)的缩写。
链表是一种支持顺序遍历的容器;而且它是一个递归的数据结构:它本身的定义是递归的。正因为这样,大部分针对它遍历算法都是递归函数。为了更好的理解这种数据结构本身和它的操作,我们必须理解以下三个概念:构造器(constructor),选择器(selector)和识别器(recognizer)。
构造器
是用来构建数据类型实例的函数。LISP中一个链表可以通过计算下面任意一个函数得到:
1.
nil
:计算nil函数会得到一个空的链表
2.
(cons x L)
:其中x是一个LISP对象(注意对象可以另一是链表),L是一个已经存在的链表。函数cons会将x插在L的前头从而构建一个新的链表。
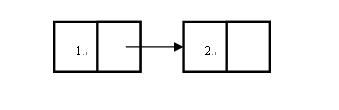
可以看得出这两个定义是递归的。例如,要构建一个包括1后面跟着2的链表,我们可以用这样的表达式:(cons 1 (cons 2 nil))。LISP会打印(1 2)来表示新构建的链表。看一下这个表达式的运算过程:nil的结果产生一个空链表;(cons 2 nil)将2插在了空链表的前头;最后(cons 1 (cons 2 nil))将1插在之前链表的前头。最后得到的链表是1->2(->nil,nil是什么都没有)。
如果要插入的元素多了,用cons就很麻烦。这里可以使用quote函数。例如: (quote (2 3 5 7 11 13 17 19))会产生这样一个链表:(2 3 5 7 11 13 17 19)。这个表达式可以方便的写成 '(2 3 5 7 11 13 17 19),符号“’”表示“quote”。
我们看看选择器。顾名思义选择器用于选择对象:它会用来返回复合结构(由多个对象组成的结构,链表也是其中一种)中的一个对象。假设L1 由(cons x L2)产生,其中x是一个LISP对象而L2 是个链表。下面选择器函数 (first L1)和(rest L1)会分别运算得出结果x 和L2 。下面是更多的例子:
[1]>: (first '(2 4 8))
2
[2]>: (rest '(2 4 8))
(4 8)
[3]>: (first (rest '(2 4 8)))
4
[4]>: (rest (rest '(2 4 8)))
(8)
[5]>: (rest (rest (rest '(8))))
NIL
最后我们看下识别器。识别器函数用于识别一个对象是由什么构造器构建的,因此,对应每一个构造器,都有一个相应的识别器。对于链表来说,构造器函数“nil”对应的识别器是“null”函数;而“cons”函数对应的是“consp” 识别器函数。对一个特定的链表L,表达式(null L)会返回t(“真”)-如果L 是由“nil”函数构建的话(就是说L是空的);而 (consp L) 会返回t(“真”)-如果L 是由“cons”构建的话。更多的例子:
[6]>: (null nil)
T
[7]>: (null '(1 2 3))
NIL
[8]>: (consp nil)
NIL
[9]>: (consp '(1 2 3))
T
注意到,由于链表来说只有两个构造器,所以链表的识别器也只有两个,它们是互补的(非此则彼)。这种情况下,表达式中只需要用到其中一个识别器就够了。
链表的结构化递归处理
理解构造器,选择器和识别器有助于我们开发递归函数。让我们先从一个例子出发。LISP有一个内置的函数“list-length”用来计算一个链表的元素个数:
[10]>: (list-length '(2 3 5 7 11 13 17 19))
8
下面我们看看这个函数是如何实现的。
一个链表L会由下面两个构造器构建-“nil”和“cons”:
- 第一种情况: L 是空的(由“nil”构建);空链表的长度是0
- 第二种情况: L 是非空的(由“cons”构建);那么:L = (first L) + (rest L)。而(first L)的长度总是1(因为它总是只有返回的第一个对象嘛),所以:L的长度 = 1 + (rest L)的长度。
因此,函数“list-length”可以这样实现:
(defun list-length1 (L)
"list-length
的递归实现"
(if (null L)
0
(1+ (list-length1 (rest L)))))
这里,我们使用了“null”函数来识别L是如何构建的。如果L是空,它的长度就是0,则返回0;如果L非空,那么它就是由“cons”构建的,它的长度就是1加上(rest L)的长度。
我们使用“”函数来追踪(注)递归调用过程:
[3]> (trace list-length1)
;; Tracing function LIST-LENGTH1.
(LIST-LENGTH1)
[4]> (list-length1 '(2 3 5 7 11 13 17 19))
1. Trace: (LIST-LENGTH1 '(2 3 5 7 11 13 17 19))
2. Trace: (LIST-LENGTH1 '(3 5 7 11 13 17 19))
3. Trace: (LIST-LENGTH1 '(5 7 11 13 17 19))
4. Trace: (LIST-LENGTH1 '(7 11 13 17 19))
5. Trace: (LIST-LENGTH1 '(11 13 17 19))
6. Trace: (LIST-LENGTH1 '(13 17 19))
7. Trace: (LIST-LENGTH1 '(17 19))
8. Trace: (LIST-LENGTH1 '(19))
9. Trace: (LIST-LENGTH1 'NIL)
9. Trace: LIST-LENGTH1 ==> 0
8. Trace: LIST-LENGTH1 ==> 1
7. Trace: LIST-LENGTH1 ==> 2
6. Trace: LIST-LENGTH1 ==> 3
5. Trace: LIST-LENGTH1 ==> 4
4. Trace: LIST-LENGTH1 ==> 5
3. Trace: LIST-LENGTH1 ==> 6
2. Trace: LIST-LENGTH1 ==> 7
1. Trace: LIST-LENGTH1 ==> 8
8
[5]>_
上面我们看到的就是结构化递归(structural recursion)- 它是一种标准的模式。对于有递归结构的数据(例如链表)X,处理过程是这样子的:
- 使用识别器来识别X 是如何被构建的;在我们的例子中,我们用“null”来识别一个链表是被“nil”还是“cons”来构建;
- 如果对象已经不能再被分解,则返回一个已知的/确定的值;例如,当一个链表已空的时候,返回它的长度0;
- 如果对象是复合结构的,则用选择器将它分解;在例子中,我们使用“first”和“rest”将链表分解成非空链表;
- 按照上面的步骤,我们不断地对X进行分解操作(递归的步骤);在例子中,我们把递归地对(rest L)进行前面的步骤;
- 最后,我们使用构造器或者其它函数将递归调用的结果汇总最终得到总的结果;在“list-length1”例子中,我们每一步都返回1加上递归调用的结果。
【注】:有时由于输出太多,阅读性会变差。这种情况下可以选择将屏幕输出输出到外部文件上(同时也会在屏幕显示)。使用“(dribble "c://output.txt")”命令将屏幕输出输出到“output.txt”文件上。要停止输出,使用命令“(dribble)”(没有参数)就行了。
符号(Symbols)
除了数字,LISP的另一种数据类型是符号。一个符号实际上就是一串字符,例如:
[1]>: 'a ; LISP
大小写不敏感
A
[2]>: 'A ; 'a
和'A被计算成同一个符号
A
[3]>: 'apple2 ;
字符,数字字符
APPLE2
[4]>: 'an-apple ;
和一些符号都是允许的
AN-APPLE
[5]>: t ;
我们熟识的t(真值)也是一个符号
T
[6]>: 't ;
另外,单引号对真值是多余的
T
[7]>: nil ; nil
也一样
NIL
[8]>: 'nil ;
加上单引号也无妨
NIL
使用符号,我们可以创建这样的链表:
[9]>: '(how are you today ?) ;
一个符号链表
(HOW ARE YOU TODAY ?)
[10]>: '(1 + 2 * x) ;
一个包含符号和数字的链表
(1 + 2 * X)
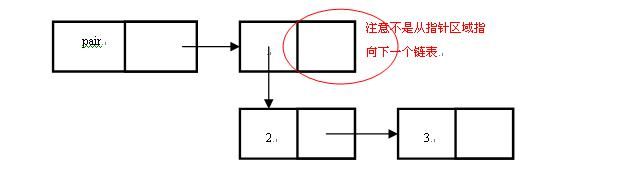
[11]>: '(pair (2 3)) ;
一个包含符号“pair”和(子)链表(2 3)的链表
(pair (2 3))
*
注意上面的链表长度为2:
[12]>: (list-length '(pair (2 3)))
2
同样:
[13]>: (first '(pair (2 3)))
PAIR
[14]>: (rest '(pair (2 3)))
((2 3))