应用Backtracking解一道算法题

应用Backtracking解一道算法题

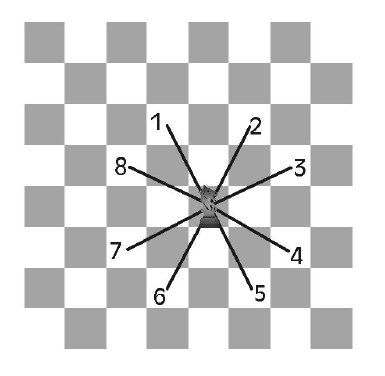
在一个n乘n的棋盘上有一匹马，要求这匹马不重复的把每个格子都跳一边。这里马的走法和中国象棋里的马一样。如下图所示，一步只能跳到位于棋盘内的1到8的八个格子里。

 

对这道题目，一个最直观的解法就是使用所谓的Backtracking的思路，从起点开始，一直跳，没格子可跳了，就退回一步，接着往下跳。在这个过程中，记下所有跳过的格子，不重复跳到跳过的格子里。直到所有的格子都跳完为止，也就是发现一个解法，或者所有可能的跳法都试过，还没有找到一个跳法，也就是没有解法。

很简单的思路，但是如果你不熟悉Recursion的编程的话，要实现却不那么简单。Recursion是计算机科学中最重要的一个概念和工具，也是计算机科学强大动力的源泉，怎么强调都不过分。Recursion在计算机的各个学科都有着非常重要的作用。所有可计算的函数可以归结在Partial Recursive Function下。掌握和熟悉Recursion的思路可以说是您步入计算机科学殿堂的第一步。

下面是我用Java编写的跳马题的Recursive的解法

 1       private   static   int [][] board;
 2       private   static   int  length;
 3 
 4       /**
 5       * search a solution of Springerproblem
 6       * 
 7       *  @param  n  board of n*n fields
 8       *  @param  x  [1 .. n] horizontal coordinate
 9       *  @param  y  [1 .. n] vertical coordinate
10       *  @return    true found, false no
11        */
12       public   static   boolean  search( int  n,  int  x,  int  y) {
13           if  (n  <   1   ||  x  <   1   ||  x  >  n  ||  y  <   1   ||  y  >  n) {
14              System.out.println( " wrong input dimension. " );
15               return   false ;
16          }
17 
18          board  =   new   int [n  +   1 ][n  +   1 ];
19          length  =  n;
20           for  ( int  i  =   1 ; i  <=  length; i ++ )
21               for  ( int  j  =   1 ; j  <  length; j ++ )
22                  board[i][j]  =   0 ;
23 
24           return  research(x, y,  1 );
25      }
26 
27       /**
28       * recursive search
29       * 
30       *  @param  x 起点x
31       *  @param  y 起点y
32       *  @param  step 第几步
33       *  @return true 找到解法，false，失败了
34        */
35       private   static   boolean  research( int  x,  int  y,  int  step) {
36           if  (x  <   1   ||  x  >  length  ||  y  <   1   ||  y  >  length)
37               return   false ;
38           if  (board[x][y]  >   0 )
39               return   false ;
40 
41          board[x][y]  =  step;
42           if  (step  ==  length  *  length)
43               return   true ;
44 
45           if  (research(x  -   1 , y  -   2 , step  +   1 ))
46               return   true ;
47           if  (research(x  -   1 , y  +   2 , step  +   1 ))
48               return   true ;
49           if  (research(x  +   1 , y  -   2 , step  +   1 ))
50               return   true ;
51           if  (research(x  +   1 , y  +   2 , step  +   1 ))
52               return   true ;
53           if  (research(x  -   2 , y  -   1 , step  +   1 ))
54               return   true ;
55           if  (research(x  -   2 , y  +   1 , step  +   1 ))
56               return   true ;
57           if  (research(x  +   2 , y  -   1 , step  +   1 ))
58               return   true ;
59           if  (research(x  +   2 , y  +   1 , step  +   1 ))
60               return   true ;
61 
62          board[x][y]  =   0 ;
63           return   false ;
64      }

 

初学Recursion的时候，很不习惯他的思维方式。有时候甚至会奇怪这样就把问题解决了。在使用Recursion编程的时候，可以假定您已经有一个要找的函数f了，然后应用f 较小的情况来解决大的情况，最小的情况另外特殊求解。这个过程中最关键的就是设计f的接口和功能，在解题的过程中，您可能要不断的调整f的接口和功能。

转载请保留 http://www.blogjava.net/xilaile/archive/2007/04/06/109001.html