后缀数组及其应用
后缀数组概念
基本概念介绍:
子串:字符串 S 的子串 r[i..j] , i ≤ j ,表示 r 串中从 i 到 j 这一段,就是顺次排列 r[i],r[i+1],...,r[j] 形成的字符串。
后缀:从某个位置 i 开始到整个串末尾结束的一个特殊子串。字符串 r 的从 第 i 个字符开始的后缀表示为 suffix(i) ,也就是suffix(i)=r[i..len(r)] 。
比如字符串:S="aabaa", 则后缀suffix(2)="baa"(下标从0开始).
字符串比较:按“字典顺序”比较,比如字符串”aaa“排列在"aab"前面。
后缀数组sa:将s的n个后缀从小到大排序后将 排序后的后缀的开头位置 顺次放入sa中,则sa[i]储存的是排第i大的后缀的开头位置。简单的记忆就是
“排第几的是谁”。 比如 字符串 S="ban" 则后缀数组有{"ban", "an", "n"}, 注意到后缀数组中只要简单的记下后缀开始的下标即可,即等价于后缀数组为
{0,1,2}, 现在需要对后缀数组进行排序排序后为{"an", "ban", "n"} 则对应的后缀数组sa为 sa={1,0,2}。sa即按字典序排列过的后缀数组,如排第一的为
sa[0]=1,第二的位sa[1]=0。
名次数组rank:rank[i]保存的是suffix(i){后缀}在所有后缀中从小到大排列的名次。则 若 sa[i]=j,则 rank[j]=i。简单的记忆就是“你排第几”。后缀数组
和名次数组为互逆 运算,有rank[ sa[i] ]=i (这是很重要的一点,通过sa与rank的关系可以求出后缀数组)。
比如 S="ban" ,后缀数组为sa={1,0,2} ,rank[i] 表示以下标i开始的后缀 在sa中的名次, 比如rank[0]=1,rank[1]=0。
构造后缀数组
最直接最简单的方法当然是把S的后缀都看作一些普通的字符串,按照一般字符串排序的方法对它们从小到大进行排序。比如利用快速排序,则在
最坏的情况下时间发杂度为O(n^2logn)(虽然比较次数是,O(nlogn),但两个字符串的比较不是O(1)的而是O(n)的),不能满足我们的需要。因为它
没有利用到各个后缀之间的有机联系,所以它的效率不可能很高。有比较好的方法比如倍增算法等,详细wiki参考 及百度百科。
其中倍增法用的比较多,建议理解使用这个方法。其基本思想就是先计算从每个位置开始的长度为2的子串的顺序,再利用这个结果计算长度为4的
子串的顺序,接下来计算长度为8的子串的顺序,不断倍增,知道长度大于等于字符串长度n 就得到 后缀数组了。
作个简单证明,假设已经求得了长度为k的子串的顺序,要求长度为2k的子串的顺序,记rank(i)为串S[i,k]在所有排序好的长度为k的子串中是第几小
的。要计算长度为2k的子串的顺序,就只要对两个rank 组成的数对进行排序就好了,我们通过rank(i)和ranK(i+k)的数对和 rank(j)和rank(j+k)的数对
的比较来替换s[i,2k]和s[j,2k]的直接比较,因为比较rank(i),rank(j)就相当于比较s[i,k]和s[j,k],比较rank(i+k),rank(j+k)就相当于比较s[i+k,k],s[j+k,j+2k]。
相当于基数排序的思想,参考。
最长公共前缀(LCP)
注意最长公共子串LCP和最长公共子序列LCS的区别。
height数组:定义height[i]=suffix(sa[i-1])和suffix(sa[i])的最长公共前缀,也就是排名相邻的两个后缀的最长公共前缀。那么对于j和k,不妨设rank[j]<rank[k],
则有以下性质:suffix(j)和suffix(k)的最长公共前缀为height[rank[j]+1],height[rank[j]+2],height[rank[j]+3],……,height[rank[k]]中的最小值。
可以看到height数组 即 高度数组 就是 后缀数组中相邻两个后缀的最长公共前缀,高度数组的计算简单,但非常巧妙。其中性质 h(i)>=h(i-1)-1 值得细细体会。
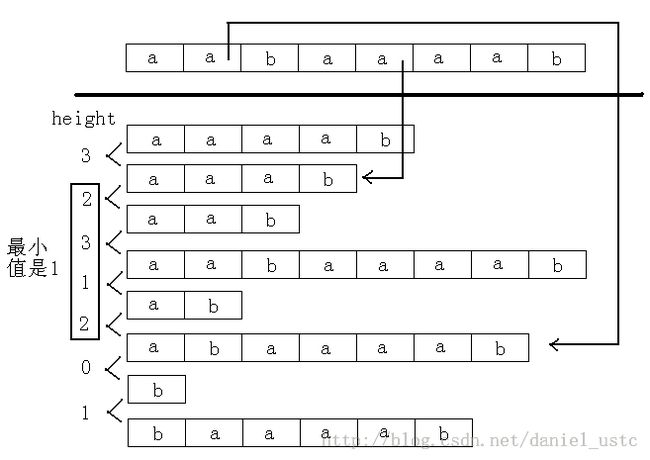
例如,字符串为“aabaaaab”,求后缀“abaaaab”和后缀“aaab”的最长公共前缀,如图所示。
那么,怎么求height数组呢,定义h[i]=height[rank[i]],也就是suffix(i)和在它前一名的后缀的最长公共前缀。h 数组有以下性质:h[i]≥h[i-1]-1,证明见老罗的论文,
就不详细说了,按照h[1],h[2],……,h[n]的顺序计算,并利用h 数组的性质,时间复杂度可以降为O(n)。h数组求出以后就可以用O(n)的时间求出height数组了。
证明可以参阅IOI国家集训队2004年论文《后缀数组》(许智磊)和IOI国家集训队2009年论文《后缀数组——处理字符串的有力工具》(罗穗骞)。
编程练习
poj 2217编程练习:
就是求最长公共子串的题目。
简化问题,两个子串的最长公共子串即 计算一个子串中至少出现两次的最长子串,答案一定在后缀数组中相邻两个后缀的公共前缀之中。
只要对两个字符串进行拼接即可,加上'$',拼接为一个字符串 S=s1$s2。
代码如下:
#include <iostream>
#include <string>
#include <algorithm>
using namespace std;
const int M = 10001;
int n,k;
int rk[M];
int tmp[M];
// 比较rk(i,i+k)和rk(j,j+k)
int cmp_sa(int i, int j)
{
if(rk[i] != rk[j])
return rk[i]<rk[j];
else
{
int ri = i+k<=n ? rk[i+k]:-1;
int rj = j+k<=n ? rk[j+k]:-1;
return ri<rj;
}
}
//计算字符串str的后缀数组
void construct_sa(string str, int *sa)
{
n = str.length();
// 初始长度为1,rk直接取字符编码
int i;
for(i=0; i<=n; ++i)
{
sa[i]=i;
rk[i] = i<n ? str[i]:-1;
}
//利用对长度为k的排序的结果对长度为2k的进行排序
for(k=1; k<=n; k <<= 1)
{
sort(sa, sa+n+1, cmp_sa);
// 先在tmp中临时存储新计算的rk,再转存回rk中
tmp[sa[0]] = 0;//排序名次从0开始 0,1,2...
//根据rk[sa[0]]的名次递推出rk[sa[1-n]]的名次
for(i=1; i<=n; ++i)// cmp_sa相同则rk[i-1],rk[i]相同
tmp[sa[i]] = tmp[sa[i-1]] + (cmp_sa(sa[i-1], sa[i])?1:0);
for(i=0; i<=n; ++i)
rk[i] = tmp[i];
}
}
// 高度数组
void get_height(string str, int *sa, int *height)
{
int i, j, h, n = str.length();
for(i=0; i<=n; ++i)
rk[sa[i]]=i;
h=0;
height[0]=0;
//从位置i开始的后缀及其前一名后缀的LCP
for(i=0; i<n; ++i)
{
if(rk[i]==0)
continue;
//求下标i开始的后缀的前一名后缀的下标j
j=sa[rk[i]-1];
if(h>0)//最长公共子串 h(i)>=h(i-1)-1
--h;
while(i+h <n && j+h<n)//h(i)
{
if(str[i+h] != str[j+h])
break;
++h;
}
height[rk[i]-1] = h;
}
}
void solve(string str, string T)
{
int sl = str.length();
str += '$'+T;
int sa[M]={0};
int height[M]={0};
construct_sa(str, sa);
get_height(str, sa, height);
int ans=0;
for(int i=0; i<str.length(); ++i)
{
if(sa[i]<sl != sa[i+1]<sl)//是否分别在2个字符串里
ans = max(ans, height[i]);
}
cout<<"Nejdelsi spolecny retezec ma delku "<<ans<<".\n";
}
int main()
{
//freopen("in.txt", "r", stdin);
string str;
string T;
int m;
cin>>m;
getchar();
while(m--)
{
getline(cin, str);
getline(cin, T);
solve(str, T);
}
return 0;
}
后缀数组都是非常有力的工具,需要好好学习。
参考资料:
算法竞赛入门经典 训练指南,挑战程序设计