Leetcode: Trapping Rain Water

Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.

For example, 
Given [0,1,0,2,1,0,1,3,2,1,2,1], return 6.

The above elevation map is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped. Thanks Marcos for contributing this image!

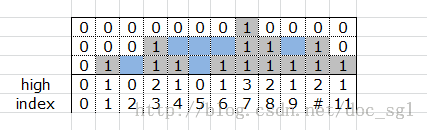
方法1：模拟

array [0,1,0,2,1,0,1,3,2,1,2,1]的矩阵如上图所示，是一个3*12的矩阵，然后从矩阵的第一行开始扫描，遇到两个1就加上这两个1之间的水量，只要扫描一遍矩阵就得到水量了，代码如下，小集合通过，大集合memory不够用。

Judge Small: Accepted!

Judge Large: Memory Limit Exceeded

int trap(int A[], int n) {
        // Note: The Solution object is instantiated only once.
        if(A==NULL || n<1)return 0;
    	int highest = A[0];
		for(int i=1;i<n;i++)
			if(A[i]>highest)highest=A[i];
		int ** matrix = new int*[highest];
		for(int i=0;i<highest;i++)
		{
			matrix[i]=new int[n];
			memset(matrix[i],0,sizeof(int)*n);
		}
		for(int i = 0; i < n; i++)
			for(int j = 1; j <= A[i]; j++)
				matrix[highest-j][i]=1;
		
		int water = 0;
		int left = -1;
		for(int i = 0; i < highest; i++)
		{
			left = -1;
			for(int j = 0; j < n; j++)
			{
				if(matrix[i][j]==1)
				{
					if(left==-1)
						left = j;
					else
					{
						water += j-left-1;
						left = j;
					}
				}
			}
		}

		for(int i=0;i<highest;i++)
			delete[] matrix[i];
		delete[] matrix;
		return water;
    }

既然memory不够，就把int矩阵改成bool吧，这样空间就由int的4byte缩小到bool的1 byte，但是还是Memory Limit Exceeded

int trap(int A[], int n) {
        // Note: The Solution object is instantiated only once.
        if(A==NULL || n<1)return 0;
    	int highest = A[0];
		for(int i=1;i<n;i++)
			if(A[i]>highest)highest=A[i];
		bool ** matrix = new bool*[highest];
		for(int i=0;i<highest;i++)
		{
			matrix[i]=new bool[n];
			memset(matrix[i],0,sizeof(bool)*n);
		}
		for(int i = 0; i < n; i++)
			for(int j = 1; j <= A[i]; j++)
				matrix[highest-j][i]=1;
		
		int water = 0;
		int left = -1;
		for(int i = 0; i < highest; i++)
		{
			left = -1;
			for(int j = 0; j < n; j++)
			{
				if(matrix[i][j])
				{
					if(left==-1)
						left = j;
					else
					{
						water += j-left-1;
						left = j;
					}
				}
			}
		}

		for(int i=0;i<highest;i++)
			delete[] matrix[i];
		delete[] matrix;
		return water;
    }

但仔细想想感觉这道题应该是扫一遍就能得到结果的。。。

对某个值A[i]来说，能trapped的最多的water取决于在i之前最高的值leftMostHeight[i]和在i右边的最高的值rightMostHeight[i]（均不包含自身）。

如果min(left,right) > A[i]，那么在i这个位置上能trapped的water就是min(left,right) – A[i]。

有了这个想法就好办了，第一遍从左到右计算数组leftMostHeight，第二遍从右到左计算rightMostHeight。

时间复杂度是O(n)。

int trap(int A[], int n) {
        // Note: The Solution object is instantiated only once.
        if(A==NULL || n<1)return 0;
    	
		int maxheight = 0;
		vector<int> leftMostHeight(n);
		for(int i =0; i<n;i++)
		{
			leftMostHeight[i]=maxheight;
			maxheight = maxheight > A[i] ? maxheight : A[i];
		}

		maxheight = 0;
		vector<int> rightMostHeight(n);
		for(int i =n-1;i>=0;i--)
		{
			rightMostHeight[i] = maxheight;
			maxheight = maxheight > A[i] ? maxheight : A[i];
		}

		int water = 0;
		for(int i =0; i < n; i++)
		{
			int high = min(leftMostHeight[i],rightMostHeight[i])-A[i];
			if(high>0)
				water += high;
		}
		return water;
    }