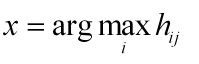NMF在文档聚类中的应用
上一篇详细说明了NMF算法。这里,来学习下NMF在文档聚类中的应用。
(1)给定一个文档语料库,首先构造一个词-文档矩阵V,其中V的i列代表文档di的加权词频向量。
(2)使用NMF方法分解矩阵V,得到分解矩阵W,H
![]()
(3)归一化W,H。
(4)使用矩阵H来决定每个文档的归类。那个文档di的类标为:x,当:
当然,如果想对单词进行聚类,我们可以通过W矩阵来确定。对于单词ti,分配的类标x,当:

上面,我们对NMF在文本聚类上的应用只是做了简要的介绍。对了,如何构造单词-文档矩阵,我们这里没详细介绍(做文本聚类的人,这个是常识哦)。
下面贴出自己编写的代码,依然采用Python脚本撰写的(为啥? 主流,方便呗):
# !/usr/bin/python
# file name : NMF
from numpy import *
from math import log
from math import sqrt
def difcost(a,b):
dif=0
for i in range(shape(a)[0]):
for j in range(shape(a)[1]):
# Euclidean Distance
dif+=pow(a[i,j]-b[i,j],2)
return dif
def difcost_KL(a,b):
dif=0
for i in range(shape(a)[0]):
for j in range(shape(a)[1]):
dif+=a[i,j]*log(a[i,j]/b[i,j])-a[i,j]+b[i,j]
return dif
# NMF
def factorize(v,pc=10,iter=50):
ic=shape(v)[0]
fc=shape(v)[1]
# Initialize the weight and feature matrices with random values
w=matrix([[random.random() for j in range(pc)] for i in range(ic)])
h=matrix([[random.random() for i in range(fc)] for i in range(pc)])
# Perform operation a maximum of iter times
for i in range(iter):
wh=w*h
# Calculate the current difference
cost=difcost_KL(v,wh)
if i==0: print cost
# Terminate if the matrix has been fully factorized
if cost==0: break
# Update feature matrix
hn=(transpose(w)*v)
hd=(transpose(w)*w*h)
h=matrix(array(h)*array(hn)/array(hd))
# Update weights matrix
wn=(v*transpose(h))
wd=(w*h*transpose(h))
w=matrix(array(w)*array(wn)/array(wd))
# normalize w,h
for j in range(pc):
sum = 0.0
for k in range(ic):
sum = sum + w[k,j]* w[k,j]
sum = sqrt(sum)
for k in range(ic):
w[k,j] /= sum
for k in range(fc):
h[j,k] /= sum
return w,h
# using NMF for clustering ;
# v is original matrix;
# k is the cluster number;
def NMF_Cluster(v,k):
w,h = factorize(v,k)
cluster = [[] for i in range(k)]
ht = transpose(h)
for i in range(shape(ht)[0]):
bestlabel = 0
max_eig = 0
for j in range(shape(ht)[1]):
if ht[i,j] > max_eig:
max_eig = ht[i,j]
bestlabel = j
cluster[bestlabel].append(i)
return cluster