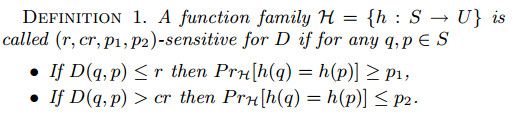【Similarity Search】Multi-Probe LSH——构建高维相似性搜索的高效索引

摘要

针对高维数据的相似性索引非常适于构建内容相关的检索系统，尤其对于音频、图像、视频等内容丰富的数据。近年来，位置敏感哈希及其变种算法以近似相似性搜索的索引技术被提出，这些方法的一个显著缺点是需要很多的哈希表来保证良好的搜索效果。该文章提出了一个新的索引策略来克服上述缺点，称作多探头LSH。
多探头LSH建立在LSH技术基础上，它可以智能地探测哈希表中可能包含查询结果的多个桶(buckets)，该方法受基于熵的LSh方法(设计用于降低基本LSH方法对空间的要求)的启发。根据评估显示，多探头LSH比起之前提出的方法在空间和时间效率上都有了显著的提高。

相似性搜索技术简介

对于高维空间的相似性搜索在数据库、数据挖掘、搜索引擎，尤其是对于像音频录音、数字照片、数字影片和其他传感器数据这些基于内容的搜索方面日益重要。由于这些特征丰富的数据常被表示为高维特征向量，相似性搜索一般应用在K近邻(K-Nearest Neighbor,KNN)和近似近邻(Approximate Nearest Neighbors,ANN)搜索中。
一个针对相似性搜索的理想索引策略需满足以下特性：

• 准确性，一个查询操作应该得到接近于暴力线性搜索的理想返回结果。
• 时间效率，一个查询操作的时间复杂度应该是O(1)或者O(logN)，其中N是数据集的数据数量。
• 空间效率，索引应该需要较少的内存空间，最好是和数据集数量差不多，不能比原始数据还要多。对于大数据集，索引结构应在主存的可容范围之内。
• 高维度，索引策略应在高维空间中工作良好。

用于KNN搜索的树索引方法，如R树、KD树、SR树、导航网(navigating nets)、覆盖树(cover tree)，虽然能返回准确的结果，但是在高维空间中难有快速的时间效率。当维度大于10之后，这些索引结构比暴力线性扫描的方法还要慢。
针对高维相似性检索算法，最有名的索引方法就是位置敏感哈希了。其基本方法是使用一组位置敏感哈希函数将在高维空间中相邻的数据映射到相同的桶之中。

• 为了进行相似性搜索，该索引方法将查询数据映射到一个桶中，使用该桶中的数据作为结果的候选集。
• 为了实现高搜索准确率，该方法需要使用多个哈希表来得到优良的候选集。
  实验研究显示，这种基本的LSH方法需要超过100个甚至几百个哈希表来实现良好的搜索准确率，由于哈希表的数量和数据量是成比例的，所以基本的方法没法满足空间效率的要求。

LSH简介

这里我将不再介绍基本的LSH原理，而只是大体的说明LSH的索引方法的框架结构，以保证与后面介绍的变种LSH方法的连贯性。
关于这一部分的详细内容可以参见：

• LSH算法框架分析
• p稳定分布LSH算法

LSH的基本思路是使用哈希函数依高概率将相似的数据映射到同一哈希桶中。
根据LSH索引，执行一次相似查询需要两个步骤：
（1）使用LSH函数对给定的查询数据q选取候选数据集。
（2）根据这些候选数据与q的距离进行排序，然后返回Top-K个数据。

由于这样的概率特性保证，可以使得两个距离较远的数据点碰撞的概率是p2^M(其中M是LSH函数的个数)，但同时也是的相邻的数据碰撞的概率是p1^M。
这样的基本的LSH索引方法需要很多哈希表来保证涵盖大部分近邻数据，这对空间要求是很大的，一旦哈希表的空间要求超过了主存的容量，我们不得不将哈希表存放在磁盘中，那么磁盘I/O的速度来查询必然大大降低了查询速度。

Entopy-based LSH介绍

Entopy-based LSH构造索引和基本的LSH策略相似，但是使用了一种不同的查询过程，该方法通过随机生成若干个与查询数据临近的扰动查询数据(perturbing query objects)，将这些数据和待查询数据一同进行哈希，将所有的结果汇总得到候选集。
Entopy-based LSH提出的对哈希桶进行采样的方法是，每一次将与查询数据q距离为Rp的随机数据p'进行哈希，得到p'所对应的哈希桶；多次进行这样的采样动作以较高概率保证所有可能的桶都被探测(probe)到。

Entopy-based LSH的不足

首先，该方法的采样过程效率不足，扰动数据的生成和其哈希值计算速度慢，并且不可避免地得到重复的哈希桶。这样，高概率被映射的桶会多次计算得到，这种计算是浪费的。
另一个缺点是，采样过程需要对近邻距离Rp有一定了解，这对于数据相互以来的情形是困难的。如果Rp过小，扰动查询数据可能无法产生足够的候选集合；如果Rp过大，就需要更多的扰动查询数据来保证更好的查询质量。

多探头LSH索引(Multi-Probe LSH Indexing)

算法概述

Multi-Probe LSH方法的关键点是，使用一个经过仔细推导出的探测序列(carefully derived probing sequence)，得到和查询数据近似的多个哈希桶。
根据LSH的性质，我们可知如果与查询数据q相近的数据没有和q被映射到同一个桶中，它很有可能被映射到周围的桶中(即两个桶的哈希值只有些许差别),所以该方法的目标是定位这些临近的桶，以便增加查找近邻数据的机会。

• 首先，我们定义一个哈希微扰向量(hash perturbation vector)Δ=(δ1,...,δM)，给定一个查询数据q，基本LSH方法得到的哈希桶是g(q)=(h1(q),...,hM(q))，我们定义微扰Δ，我们可以探测到哈希桶g(q)+Δ。
• 回想LSH函数
  
  
  如果我们选择合理的W，那么相似的数据应该映射到相同或者临近的哈希值上（较大的W使得这个值相差最多一个单位），因此，我们关注微扰向量Δ在δi={-1，0，1}。
• 微扰向量直接作用于查询数据的哈希值上，避免了Entopy-based LSH方法中扰动数据计算和哈希值计算的天花板问题(overhead)。该方法设计的微扰向量序列(a sequence of pertubation vectors)中，每个向量都映射成一个唯一的哈希值集合，这样就不会重复探测一个哈希桶了。

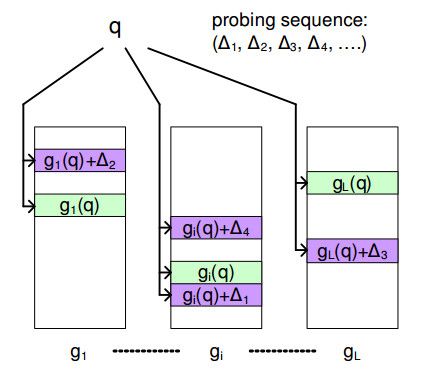
下面的图片演示了Multi-Probe LSH方法：

其中，gi(q)是第i个哈希表中查询数据q的哈希值；(Δ1,Δ2,...)是探测序列(probing sequence)；gi(q)+Δ1是使用Δ1附加到gi(q)的新的哈希值，它指向了该哈希表中其他的哈希桶。
通过使用多个微扰向量，我们可以定位多个哈希桶，以便获得查询值q的更多的近邻候选项。

参考资料

• R. Panigrahy. Entropy based nearest neighbor search in high dimensions. In Proc. of ACM-SIAM Symposium on Discrete Algorithms(SODA), 2006
• Multi-Probe LSH: Efficient Indexing for High-Dimensional Similarity Search by Qin Lv, William Josephson, Zhe Wang, Moses Charikar, Kai Li., Proceedings of the 33rd International Conference on Very Large Data Bases (VLDB). Vienna, Austria. September 2007

转载请注明作者Jason Ding及其出处
Github博客主页(http://jasonding1354.github.io/)
CSDN博客(http://blog.csdn.net/jasonding1354)
简书主页(http://www.jianshu.com/users/2bd9b48f6ea8/latest_articles)
百度搜索jasonding1354进入我的博客主页