ACM-计算几何之Cupid's Arrow——hdu1756

Cupid's Arrow

题目：http://acm.hdu.edu.cn/showproblem.php?pid=1756

Problem Description

传说世上有一支丘比特的箭，凡是被这支箭射到的人，就会深深的爱上射箭的人。
世上无数人都曾经梦想得到这支箭。Lele当然也不例外。不过他想，在得到这支箭前，他总得先学会射箭。
日子一天天地过，Lele的箭术也越来越强，渐渐得，他不再满足于去射那圆形的靶子，他开始设计各种各样多边形的靶子。
不过，这样又出现了新的问题，由于长时间地练习射箭，Lele的视力已经高度近视，他现在甚至无法判断他的箭射到了靶子没有。所以他现在只能求助于聪明的Acmers，你能帮帮他嘛？

Input
本题目包含多组测试，请处理到文件结束。
在每组测试的第一行，包含一个正整数N(2<N<100),表示靶子的顶点数。
接着N行按顺时针方向给出这N个顶点的x和y坐标(0<x,y<1000)。
然后有一个正整数M，表示Lele射的箭的数目。
接下来M行分别给出Lele射的这些箭的X,Y坐标(0<X,Y<1000)。

Output
对于每枝箭，如果Lele射中了靶子，就在一行里面输出"Yes",否则输出"No"。

Sample Input
4
10 10
20 10
20 5
10 5
2
15 8
25 8

Sample Output
Yes

No

这道题也是判断点是否在多边形内，这次来说一下射线法。。

之前说了一个O（logn）的二分法，详情可戳：http://blog.csdn.net/lttree/article/details/24291719

射线法：

这张图片比较全啊。

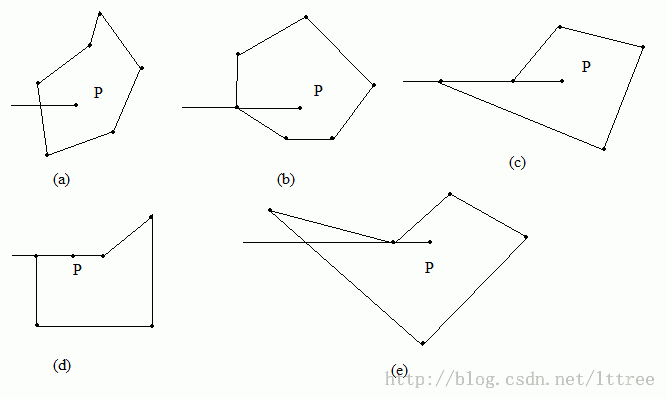
我们以所求点为原点向任意方向做一条射线，如果点在多边形内，做的射线肯定会与多边形的某条边相交。（如a所示），因为多边形可能为凹多边形，所以如果交点有一个则为点在多边形内，若有2个交点则点在多边形外。

以此类推，奇数个点代表点在多边形内，偶数个点代表点在多边形外。

但是还是有几个特殊情况要处理一下：

①射线经过的是多边形端点，如图b

②射线经过多边形某条边，如图c

③射线经过多边形端点和边，如图d

④射线经过端点且边，如图e

我们的解决方法：（序号顺序并非解决相应问题方法）

①对于多边形平行边，不考虑它。

②对于多边形的顶点和射线相交的情况，如果该顶点是其所属边上纵坐标较大的顶点，则计数，否则，忽略该点。

③对于所求的点在多边形边上的情况，直接判断点属于多边形。

And now 让我们一起AC~

PS：不要忘了精度问题哈~

#include <stdio.h>
#define MAX 100001
// 需要精度判断
#define EPS 1e-8
struct point
{
    double x,y;
}p[MAX];
// 比较大小函数
double Max(double a,double b)    { return a>b?a:b; }
double Min(double a,double b)    { return a>b?b:a; }
double abs(double a)    {   return a<0?-a:a; }
// 两个向量的叉积
double cross(double x,double y,double xx,double yy)
{
    return x*yy-y*xx;
}
// 判断点是否在直线上，叉积为0，且满足坐标相对位置条件
bool online(point a,point b,point c)
{
    if( abs( cross(a.x-b.x,a.y-b.y,c.x-b.x,c.y-b.y) )<EPS &&
       a.x>=Min(b.x,c.x) && a.x<=Max(b.x,c.x) &&
       a.y>=Min(b.y,c.y) && a.y<=Max(b.y,c.y) )
        return 1;
    return 0;
}

int main()
{
    int i,n,m,js,flag;
    point a,b,c,d;
    while( scanf("%d",&n)!=EOF )
    {
        // 先输入多边形各个点（此题按顺时针输入
        for(i=0;i<n;++i)
            scanf("%lf%lf",&p[i].x,&p[i].y);
        scanf("%d",&m);
        while(m--)
        {
            flag=js=0;
            // 输入所求点坐标
            scanf("%lf%lf",&a.x,&a.y);
            b.x=-100,b.y=a.y;


            for(i=0; i<n; ++i)
            {
                c.x=p[i].x;
                c.y=p[i].y;
                d.x=p[ (i+1)%n ].x;
                d.y=p[ (i+1)%n ].y;

                // 判断点是否在线上
                if(online(a,c,d))
                {
                    flag=1;
                    break;
                }
                // 第一个判断：是否平行边，后面两个a点纵坐标在两端点之间，而且<=最大的端点（因为解决方法中②）
                // 第二个判断为判断线段相交，注意精度判定
                if( c.y!=d.y && a.y>Min(c.y,d.y) && a.y<=Max(c.y,d.y) )
                    if( cross(a.x-d.x,a.y-d.y,c.x-d.x,c.y-d.y)*cross(b.x-d.x,b.y-d.y,c.x-d.x,c.y-d.y)<EPS )
                        ++js;
            }
            // 判断交点奇偶
            if(js&1)    flag=1;
            if(flag)    printf("Yes\n");
            else    printf("No\n");
        }
    }
    return 0;
}