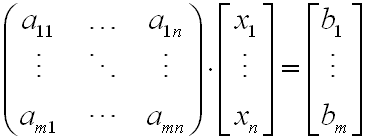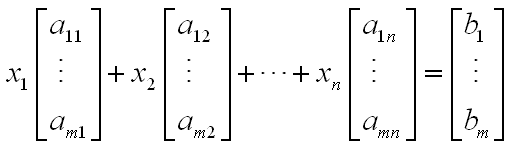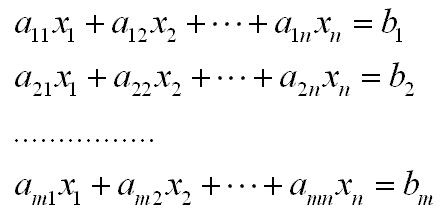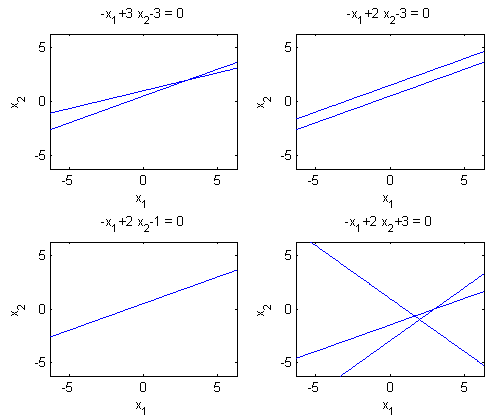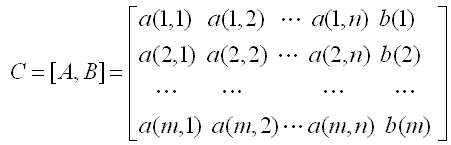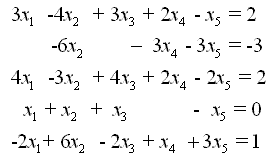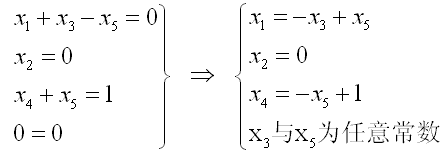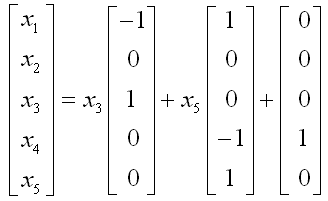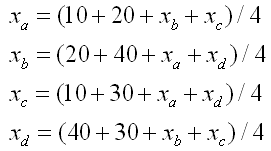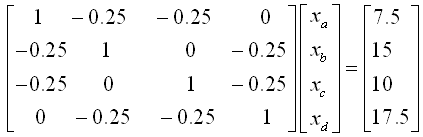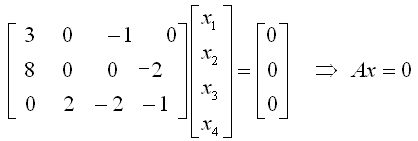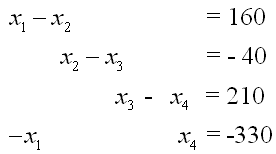原文:http://www.cnblogs.com/JCSU/articles/1449986.html
一、线性代数基本方程组
基本方程组:
矩阵表示:
解决问题的视角:
1、解联立方程的视角 (行阶梯变换 & 矩阵运算)
着重研究解x,即研究线性方程组的解法。中学里的解方程和MATLAB的矩阵除法就是这样。
要点:矩阵的每一行代表一个方程,m行代表m个线性联立方程。 n列代表n个变量。如果m是独立方程数,根据m<n、m=n、m>n确定方程是 ‘欠定’、‘适定’ 还是 ‘超定’。对这三种情况都会求解了,研究就完成了。必须剔除非独立方程。行阶梯形式、行列式和秩的概念很大程度上为此目的而建立。
2、向量空间中向量的合成的视角 (用向量空间解方程组)
把A各列看成n个m维基本向量,线性方程组看成基向量的线性合成:
要点:解x是这些基向量的系数。它可能是常数(适定方程),也可能成为其中的一个子空间(欠定方程) 。要建立其几何概念,并会求解或解空间。
3、线性变换或映射的视角 (线性变换及其特征)
把b看成变量y,着重研究把Rn空间的x变换为Rm空间y 的效果,就是研究线性变换系数矩阵A的特征对变换的影响。
要点:就是要找到适当的变换,使研究问题的物理意义最为明晰。特征值问题就是一例。
-
Leontief教授把美国的经济用500个变量的500个线性方程来描述,在1949年利用当时的计算机解出了42×42的简化模型,使他于1973年获得诺贝尔经济奖,从而大大推动了线性代数的发展。
-
把飞行器的外形分成若干大的部件,每个部件沿着其表面又用三维的细网格划分出许多立方体,这些立方体包括了机身表面以及此表面内外的空气。对每个立方体列写出空气动力学方程,其中包括了与它相邻的立方体的共同边界变量,这些方程通常都已经简化为线性方程。对一个飞行器,小立方体的数目可以多达400,000个,而要解的联立方程可能多达2,000,000个。
-
飞行器的运动要用三个转动和三个平移共六个变量来表示(像在第九章中介绍的那样)。除此以外,为了控制飞行器的三维转动,需要三个控制面,即方向舵(垂直尾翼)、升降舵(水平尾翼)和副翼,它们的偏转角又构成了三个变量。描述飞行器的运动就需要12个变量的组合。而且这已经不单是代数方程,而是微分方程了。
-
卫星上用三种可见光和四种红外光进行摄像,对每一个区域,可以获得七张遥感图象。利用多通道的遥感图可以获取尽可能多的地面信息,因为各种地貌、作物和气象特征可能对不同波段的光敏感。而在实用上应该寻找每一个地方的主因素,成为一张实用的图象。每一个象素上有七个数据,形成一个多元的变量数组,在其中合成并求取主因素的问题,就与线性代数中要讨论的特征值问题有关。
-
在全国设立几十万个观察点,把每一点的经度、纬度和高度三个坐标建立起来。现在对于经度纬度的测量精度要求,已经提高到了若干厘米,对于高度的精度要求更高。在一些边远地区,对于一些特征点的测量,要耗费很大的人力物力。例如对珠穆朗玛峰顶高度的测量,要经过多种方法,取得多种数据,并且用最小二乘法进行误差的处理。
三、行阶梯法解线性方程
1、线性方程的Matlab表示方法
(1) 由n个变量组成的m个联立线性代数方程组:
用MATLAB语言表示为:
其中:
n是未知数个数,m是独立方程的个数。当m<n时,方程组有无数多个解,称为欠定方程;当m>n时,方程组无解,称为超定方程;当m=n时,方程组有唯一解,称为适定方程;所以不能简单地看形式上的m和n,还必须剔除其中非独立方程的虚假成分。将要讨论的行阶梯形式、行列式和“秩”等概念,很大程度上就是为了找到独立方程的数目。
(2) 解线性方程组及在matlab中的显示
作图的matlab代码:
ezplot('x1-2*x2+1') %画(a)中的x1-2*x2+1=0
hold on
ezplot('-x1+3*x2-3')
subplot(2,2,2) %作右上角图,画方程组(b)
ezplot('x1-2*x2+1')
hold on
ezplot('-x1+2*x2-3')
subplot(2,2,3) %作左下角图,画方程组(c)
ezplot('x1-2*x2+1')
hold on
ezplot('-x1+2*x2-1')
subplot(2,2,4) %作右下角图,画方程组(d)
ezplot('x1+x2-1')
hold on
ezplot('x1-x2-3')
hold on
ezplot('-x1+2*x2+3')
使用参考:ezplot
四个方程组在matlab中的作图:
2、初等行变换
将系数矩阵A和B组成增广矩阵:
对增广矩阵的行作以下三种运算不会改变方程组的解,这三种运算组成了矩阵的初等行变换:
(1) 行交换:将增广矩阵的第 i , j 两行互换位置。MATLAB语句:c([i,j],:) = c([j,i],:)
(2) 行乘数:将增广矩阵的第 i 行乘以常数 k 。MATLAB语句:c(i,:) = k*c(i,:)
(3) 行相加:将增广矩阵的第 i 行乘以常数 k,加到第 j 行。MATLAB语句:c(j,:) = c(j,:) + k*c(i,:)
3、行阶梯矩阵的生成(高斯消元过程)
(1) 行阶梯矩阵、简化行阶梯矩阵
如果线性方程组的左端系数具有以下三个特点:
a) 所有非零行都处在全零行的上方;
b) 各行的第一个非零元素的列号比其上方所有各行的第一非零元素的列号都要大;
c) 所有的第一非零元素所在的列中,其下方的所有元素均为零;
这样的矩阵称为行阶梯矩阵(或上三角矩阵),如矩阵C1:
如果行阶梯矩阵还满足以下两个额外特点,则称之为简化行阶梯矩阵,如下图的矩阵C2:
1) 各行的第一个非零元素是所在列中唯一的非零元素
2) 各行的第一个非零元素都等于1
(2) 高斯消元过程、实例、matlab消元
步骤1:把主对角线下方第一列元素全变为零。在矩阵的各行中,选择第1列元素的绝对值最大的行,通过行交换把它放到第1行(这样做主要是为了提高计算精度,如果不考虑精度,只要第1行第1列元素不为零,可以跳过这个环节)。以第1行为基准,依次把第2行至第n行的第1列的元素消为零。
步骤2:在2~n行中,选择第2列元素的绝对值最大的行,通过行交换把它放到第2行。以第2行为基准行,依次把第3行至第n行的第2列的元素消为零。
步骤3: 做法同前面的步骤
...
步骤n-1:做法同前面的步骤
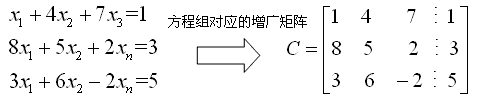
实例:用行阶梯及回代法求解以下方程组(方程组对应的增广矩阵已给出):
matlab消元程序:
% ---------------------------------
% A为输入矩阵,B为变换后的输出矩阵
% i为基准行的行号
% j为待变换行的行号
% q为基准元的列号,即A(i,q)为基准元,A(j,q)为待消元
%
x = A(i,:); y=A(j,:); % 取出A的第i,j两行命名为x,y,
z = y - y(q)/x(q)*x; % 实现(6.2.5)式的运算
A(j,:)=z; % 把结果赋值给A第j行,
B=A; % 将A作为输出变元B
matlab中的消元过程如下:
C =
1 4 7 1
8 5 2 3
3 6 -2 5
>> B=gauss(C,1,2,1) %以第1行为基准行,使第2行的第1列元素变为0
B =
1 4 7 1
0 -27 -54 -5
3 6 -2 5
>> B=gauss(B,1,3,1) %以第1行为基准行,使第3行的第1列元素变为0
B =
1 4 7 1
0 -27 -54 -5
0 -6 -23 2
>> B=gauss(B,2,3,2) %以第2行为基准行,使第3行的第2列元素变为0,此时,生成了行阶梯矩阵
B =
1.0000 4.0000 7.0000 1.0000
0 -27.0000 -54.0000 -5.0000
0 0 -11.0000 3.1111
>> B=gauss(B,3,2,3) %以第3行为基准行,使第2行的第3列元素变为0
B =
1.0000 4.0000 7.0000 1.0000
0 -27.0000 0 -20.2727
0 0 -11.0000 3.1111
>> B=gauss(B,3,1,3) %以第3行为基准行,使第1行的第3列元素变为0
B =
1.0000 4.0000 0 2.9798
0 -27.0000 0 -20.2727
0 0 -11.0000 3.1111
>> B=gauss(B,2,1,2) %以第2行为基准行,使第1行的第2列元素变为0,此时,A阵变成了对角矩阵
B =
1.0000 0 0 -0.0236
0 -27.0000 0 -20.2727
0 0 -11.0000 3.1111
>> B(2,:)=-1/27*B(2,:) %第2行除以对角项
B =
1.0000 0 0 -0.0236
0 1.0000 0 0.7508
0 0 -11.0000 3.1111
>> B(3,:)=-1/11*B(3,:) %第3行除以对角项,此时,生成了简化行阶梯矩阵
B =
1.0000 0 0 -0.0236
0 1.0000 0 0.7508
0 0 1.0000 -0.2828
>>
4、MATLAB中的行阶梯生成函数
MATLAB已经把“简化行阶梯形式(reduced row echelon form)”的计算过程集成为一个子程序rref。它的输入变元可以是线性方程组的系数矩阵,也可以是其增广矩阵,输入U=rref([A,b]),输出结果就是简化行阶梯矩阵。
例:用MATLAB中的rref求解3(2)中的方程组:
U =
1.0000 0 0 -0.0236
0 1.0000 0 0.7508
0 0 1.0000 -0.2828
>>
解得:x1=-0.0236, x2=0.7508, x3=-0.2828
5、行阶梯法解欠定方程组
上面讨论的是方程数m与变量数n相等的情况。普遍情况下,m<n,属于欠定方程,方程将有无数解,我们必须找出其解的一般形式。即使m=n,也有可能是假象,因为有的方程是相依的,有效方程数也许小于m。要看清它究竟是什么类型,应该看行阶梯形式的结果,即有效行的数目,有效行的个数也叫矩阵的“秩”。对于一个矩阵,尽管因变换的次序不同,但“秩”是唯一的。
对增广矩阵C=[A, b]进行行阶梯变换,得到的行阶梯矩阵U的下方可能有全零出现。行阶梯形式为:
其中,U为方程中左端的系数矩阵,d为方程右端的常数项。当U中某行各变量系数全为零时,d中的对应行也必须为零,否则就构成了等式左右不相等的矛盾方程。因此,矩阵A和增广矩阵[A,b]的行阶梯形式U(或简化行阶梯矩阵)应当有同样的全零行,也就是两者有同样的秩,这是方程组有解的必要条件。
原来的m行中只剩下r个非全零行,意味着m个方程中只有r个有效,也就是它的秩为r,m-r个全零行反映了原方程组中有m-r个是相依方程,最后U中有效的部分是r×n矩阵,就是r个方程和n个未知数。因为r<n,这是一个欠定方程组,n个未知数(变量)中有n-r个可以任意设定,我们称这些未知数为自由变量,也可把它们称为任意常数。
例:解下列方程组
输入系数矩阵A和常数矩阵b,求增广矩阵的简化行阶梯形式,MATLAB代码如下:
b=[2;-3;2;0;1];
B=[A,b] %增广矩阵
[U0,V0I]=rref(B) %U0存放增广矩阵的简化行阶梯形式,V0I存放各行中第一个非零元素的列号
U=U0(1:5,1:5),d=U0(:,6) %从U0中取出系数矩阵的简化行阶梯形式放入U中,常数部分放到d中
运行过程如下:
3 -4 3 2 -1 2
0 -6 0 -3 -3 -3
4 -3 4 2 -2 2
1 1 1 0 -1 0
-2 6 -2 1 3 1
U0 =
1 0 1 0 -1 0
0 1 0 0 0 0
0 0 0 1 1 1
0 0 0 0 0 0
0 0 0 0 0 0
V0I =
1 2 4
U =
1 0 1 0 -1
0 1 0 0 0
0 0 0 1 1
0 0 0 0 0
0 0 0 0 0
d =
0
0
1
0
0
>>
从U0可知,下方有两个全零行,说明原方程中有两个方程是相依的,只有三个独立方程,此时各行首非零元素不在对主角线上,列号分别为1,2,4。我们应当把x1, x2, x4看作待求的变量,而把其余的两个变量x3和x5看作自由变量。
把U恢复成方程形式并移项,使左端只包含待求变量,把x3和x5移到等式右边:
如果要给出一个具体解,通常取自由变量x3和x5为零,这样得出的解是x1=x2=x3=x5=0, x4=-1。但这样来表示方程的解容易造成误会,以为方程组只有一个解。所以比较严格的表示方法是取自由变量x3和x5为c1和c2:
x3=c1, x5=c2, x1=-c1+c2, x2=0, x4=-c2+1
这样,选择不同的c1和c2,就可以得出不同的解,所以其解有无数组。由于它包含两个自由变量,因此在两个自由度上都可以在(-∞,+∞)范围内变化,从几何上说,它的解占据了一个两维空间(平面)。
解的最后形式:
5、应用实例
(1) 平板稳态温度的计算
研究一个平板的热传导问题,设该平板的周边温度已经知道(见下图),现在要确定板中间4个点a,b,c,d处的温度。假定其热传导过程已经达到稳态,因此在均匀的网格点上,各点的温度是其上下左右4个点的温度的平均值。
根据题意列出方程为:
移项整理为标准的矩阵形式为:
输入MATLAB程度计算为:
A =
1.0000 -0.2500 -0.2500 0
-0.2500 1.0000 0 -0.2500
-0.2500 0 1.0000 -0.2500
0 -0.2500 -0.2500 1.0000
>> b=[7.5;15;10;17.5]
b =
7.5000
15.0000
10.0000
17.5000
>> U=rref([A,b])
U =
1.0000 0 0 0 20.0000
0 1.0000 0 0 27.5000
0 0 1.0000 0 22.5000
0 0 0 1.0000 30.0000
>>
把它“翻译”为方程,即有:xa=20℃,xb=27.5℃,xc=22.5℃,xd=30℃
(2) 化学方程式配平
建立一个向量方程组,每个方程分别描述一种原子在反应前后的数目。在上面的方程中,有碳、氢、氧三种元素需要配平,构成了三个方程。而有四种物质,其数量用四个变量x1,x2,x3,x4来表示。将每种物质中的元素原子数按碳、氢、氧顺序排列,可以写出:
要使方程配平,x1,x2,x3,x4必须满足:
写成矩阵方程:
对A进行行阶梯变换:
A =
3 0 -1 0
8 0 0 -2
0 2 -2 -1
>> U=rref(A)
U =
1.0000 0 0 -0.2500
0 1.0000 0 -1.2500
0 0 1.0000 -0.7500
>>
要注意这四个列对应于四个变量的系数,所以这三行系数对应的方程是:
x1 -0.2500x4 = 0
x2 -1.2500x4 = 0
x3 -0.7500x4 = 0
即x4是自由变量。因为化学家们喜欢把方程的系数取为最小整数,此处可取x4=4,则x1,x2,x3均有整数解,x1=1, x2=5, x3=3。
对于比较复杂的反应过程,为了便于得到最小整数解,在解化学配平的线性方程组时,应该在MATLAB中先规定取有理分式格式,即先输入format rat,这样就很容易看出应令x4=4。结果为:
>> U=rref(A)
U =
1 0 0 -1/4
0 1 0 -5/4
0 0 1 -3/4
>>
(3) 交通流量分析
某城市有两组单行道,构成了一个包含四个节点A,B,C,D的十字路口,如下图所示。在交通繁忙时段的汽车从外部进出此十字路口的流量(每小时的车流数)标于图上。现要求计算每两个节点之间路段上的交通流量x1, x2, x3, x4。
解:
在每个节点上,进入和离开的车数应该相等,这就决定了四个节点的流通方程:
A =
1 -1 0 0
0 1 -1 0
0 0 1 -1
-1 0 0 1
>> b=[160;-40;210;-330]
b =
160
-40
210
-330
>> U=rref([A,b])
U =
1 0 0 -1 330
0 1 0 -1 170
0 0 1 -1 210
0 0 0 0 0
>>