形式语言与自动机之语言识别机器——有穷状态自动机

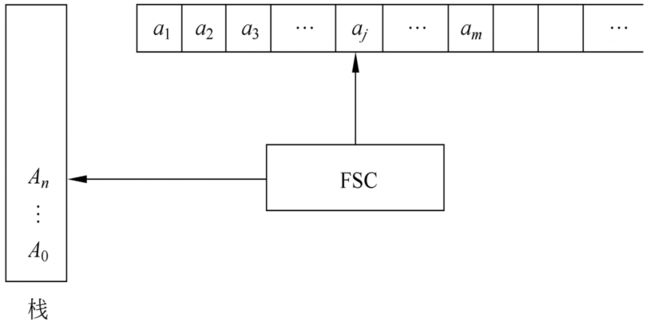
有穷状态自动机的物理模型

 

• 有穷状态自动机(finite automaton,FA)

M=(Q，∑，δ，q0，F)

Q——状态的非空有穷集合。"q∈Q，q称为M的一个状态(state)。

∑——输入字母表(Input alphabet)。输入字符串都是∑上的字符串。

q0——q0∈Q，是M的开始状态(initial state)，也可叫做初始状态或者启动状态。

δ——状态转移函数(transition function)，有时候又叫做状态转换函数或者移动函数。δ：Q×∑®Q，对"(q，a)∈Q×∑，δ(q，a)=p表示：M在状态q读入字符a，将状态变成p，并将读头向右移动一个带方格而指向输入字符串的下一个字符。

F——FÍQ，是M的终止状态(final state)集合。"q∈F，q称为M的终止状态，又称为接受状态(accept state)。  

 

下面是一个有穷状态自动机

M2=({q0，q1，q2，q3}，{0，1，2}，δ2，q0，{q2})

δ2(q0,0)= q1，δ2(q1,0)= q2

δ2(q2,0)= q1，δ2(q3,0)= q3

δ2(q0,1)= q3，δ2(q1,1)= q3

δ2(q2,1)= q3，δ2(q3,1)= q3

δ2(q0,2)= q3，δ2(q1,2)= q3

δ2(q2,2)= q3，δ2(q3,2)= q3

 

• 确定的有穷状态自动机
  • 由于对于任意的q∈Q，a∈∑，δ(q，a)均有确定的值，所以，将这种FA称为确定的有穷状态自动机(deterministic finite automaton，DFA)

• 例1:构造一个DFA，它接受的语言为{x000y|x，y∈{0，1}*}

q0——M的启动状态；

q1——M读到了一个0，这个0可能是子串“000”的第1个0；

q2——M在q1后紧接着又读到了一个0，这个0可能是子串“000”的第2个0；

q3——M在q2后紧接着又读到了一个0，发现输入字符串含有子串“000”；因此，这个状态应该是终止状态。

δ(q0,1)= q0——M在q0读到了一个1，它需要继续在q0 “等待”可能是子串“000”的第1个0的输入字符0；

δ(q1,1)= q0——M在刚刚读到了一个0后，读到了一个1，表明在读入这个1之前所读入的0并不是子串“000”的第1个0，因此，M需要重新回到状态q0，以寻找子串“000”的第1个0；

δ(q2,1)= q0——M在刚刚发现了00后，读到了一个1，表明在读入这个1之前所读入的00并不是子串“000”的前两个0，因此，M需要重新回到状态q0，以寻找子串“000”的第1个0；

δ(q3,0)= q3——M找到了子串“000”，只用读入该串的剩余部分。

δ(q3,1)= q3——M找到了子串“000”，只用读入该串的剩余部分。

M=({q0，q1，q2，q3}，{0，1}，{ (q0,0)= q1，δ(q1,0)= q2，δ(q2,0)= q3，δ(q0,1)= q0，δ(q1,1)= q0，δ(q2,1)= q0，δ(q3,0)= q3，δ(q3,1)= q3}，q0，{q3})

DFA图:

• 不确定的有穷状态自动机(non-deterministic finite automaton ,NFA)

   M是一个五元组

M=(Q，∑，δ，q0，F)

• Q、∑、q0、F的意义同DFA。
• δ：Q×∑®2Q，对"(q，a)∈Q×∑，δ(q，a)= {p1，p2，…，pm}表示M在状态q读入字符a，可以选择地将状态变成p1、或者p2、…、或者pm，并将读头向右移动一个带方格而指向输入字符串的下一个字符。 

• 接受{x|x∈{0，1}*，且x含有子串00或11}的NFA对应的移动函数定义表。

• NFA状态函数表

NFA和DFA之间是可以相互转换的：

例 2将所示的NFA对应的DFA

 

 

 

 

 NFA的

• 带空移动的不确定的有穷状态自动机(non-deterministic finite automaton with ε-moves,ε-NFA)

• ε-NFA转换为NFA

 

转换得到的NFA