POJ 1185 炮兵阵地(想半天没有想通,转一个解释)
炮兵阵地
| Time Limit: 2000MS | Memory Limit: 65536K | |
| Total Submissions: 2762 | Accepted: 776 |
Description
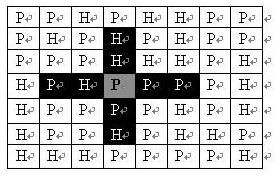
如果在地图中的灰色所标识的平原上部署一支炮兵部队,则图中的黑色的网格表示它能够攻击到的区域:沿横向左右各两格,沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。
现在,将军们规划如何部署炮兵部队,在防止误伤的前提下(保证任何两支炮兵部队之间不能互相攻击,即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内),在整个地图区域内最多能够摆放多少我军的炮兵部队。
Input
接下来的N行,每一行含有连续的M个字符('P'或者'H'),中间没有空格。按顺序表示地图中每一行的数据。N <= 100;M <= 10。
Output
Sample Input
5 4
PHPP
PPHH
PPPP
PHPP
PHHP
Sample Output
6
Source
Noi 01
分析一 盲目搜索
初学者一般看到此题估计会无从着手。如果用“万能”的搜索算法,回溯或者枚举所有的状态来求解的话,那算法复杂度将是O(2^(m*n))。
又考虑到m<=10,n<=100,这将是个及其恐怖的工作。
大家知道凡是指数级的算法一般不能作用于较大数据的运算。
分析二 动态规划
观察地图,对于任何一行的炮兵放置都与其上下几行的放置有关。如果我们逐行的放置炮兵,并且每次都知道前面每行所有放置法的最优解(即最大炮兵数),那么我们要求放置到当行时某种放置法的最优解,就可以枚举前面与其兼容(即不会发生冲突)的所有放置法,从中求得本行的最优解。
那么就可以把N*M行的最优解装换成了(N-1)*M行的最优解。此算法的基础在于,每行的状态(炮兵放置情况)只与前几行的状态有关。
这满足最优子问题和无后效性的性质,因此可以使用动态规划求解。
最优子问题大家都知道。无后效性就是指最优解只与状态有关,而与到达这种状态的路径无关。
此问题的状态就是指该行的炮兵放置法
动态方程
f[i][j][k] = max{f[i-1][k][p]+c[j]},(枚举p的每种状态)
f[i][j][k]表示第i行状态为s[j],第i-1行状态为s[k]的最大炮兵数,且s[j],s[k],s[p]及地形之间互不冲突
算法复杂度:O(N*S*S*S),N为行数,S为总状态数
问题如何描述
好了,思路大致都准备好了。但如何描述问题呢?
动态规划的关键就在于如何描述状态。如何用二进制串表示状态的话,那么在代码中表示起来将很复杂,不利于编写代码。
怎么办?
状态压缩
现在引入最关键的感念,状态压缩
我们把一个二进制串的相应十进制数称为该二进制串的压缩码,这就将一个二进制串压缩为一个简单的十进制状态。
伴随着这个概念而来的是其相应的位运算,&, |, !,<<, >>等。
相关运算
我们现在就可以用与运算&判断两个压缩状态间、压缩状态与压缩地图间是否冲突。
用移位运算>>和求余运算%计算压缩状态所包含的炮兵数
困惑?
现在似乎大功告成了,但是所写的代码提交运行结果为,Time Limit Exceed,即超时。
为什么呢?
复杂度解析
看看题目条件吧!Time Limit: 2000MS Memory Limit:65536K
我们采用压缩二进制方式来表示一行的所有状态,那么会有每行会有2^10即1024个状态。因此在最坏情况下(M=10,N=100,所有地点都是平原),会将扫描100*1024*1024*1024(10^11,远远超过2S),因此不可取。
O(N*S*S*S)不可取么?
算法加速
不!
仔细分析,状态数S真的是2^10么?
显然,有些是伪状态,自身就是个矛盾体。那么可以提前摒弃这些伪状态。记过计算,单独一行(10列)的合法状态数只有60个!!
求合法状态的代码段
sNum = 0; //合法状态总数
for ( int k = 0; k < (1<<column); k++ ){
int m = k;
//判断该状态是否合法
if ( ( (m<<1)&k ) || ( (m<<2)&k ) )
continue;
//该合法状态数包含的炮兵数
c[sNum] = m%2;
while ( m = (m>>1) ) c[sNum] += m%2;
s[sNum++] = k; //合法状态数
}
优化
考虑到本行最优解f[i][j][k]只与前一行f[i-1][k][p]有关,也就是说每次计算只需要前一行的最优解就可以了。
那只用申请f[2][61][61]的内存,就可以实现该算法,而非f[100][61][61],更非f[100][1025][1025]。
可是,如果用向量f[0]表示当前行的最优解,向量f[1]表示前一行的最优解,那每次迭代计算时岂不是又要交换两个向量的值?
滚动数组
借助滚动数组技术,可以轻松实现这个转换!
引入迭代坐标roll,向量f[roll]指向当前行,计算f[roll]时,f[(roll+1)%2]指向前一行,计算结束后,令roll = (roll+1)%2,就可以实现行转换了。
我们只要初始roll = 0即可,运算结束时,我们不必知道roll的值,但roll必然指向待计算的那行,(roll+1)%2指向最终结果所在行。
运行结果
Problem: 1185 User: new_star
Memory: 316K Time: 235MS
Language: G++ Result: Accepted
小结
1.最优子结构和无后效性
2.压缩状态的动态规划
3.位运算
4.滚动数组
实现了一个暂时没有用滚动数组的代码:
#include<stdio.h>
#include<memory.h>
#include<algorithm>
#define MAX_ROW 110
#define MAX_STATUS 70
using namespace std;
int g_Hilly[MAX_ROW];
int g_DP[MAX_ROW][MAX_STATUS][MAX_STATUS];
int g_LegalStatus[MAX_STATUS];
int g_nGunForStatus[MAX_STATUS];
bool StatusTestForRow(int nStatus)
{
return !( ((nStatus << 2) & nStatus) || ((nStatus << 1) & nStatus) );
}
int GetAllLegalStatus(int nCol)
{
int i;
int iLegalStatus = 0;
int k, nGun;
for( i = 0 ; i < (0x1 << nCol); i++)
{
if(StatusTestForRow(i))
{
k = i;
nGun = 0;
while(k)
{
k = k & (k-1);
nGun++;
}
++iLegalStatus;
g_nGunForStatus[iLegalStatus] = nGun;
g_LegalStatus[iLegalStatus] = i;
}
}
return iLegalStatus;
}
//test the cannons with the geographic and itself
bool TestIsLegalStatus(int nStatus, int iRow)
{
return (!(nStatus & g_Hilly[iRow]));
}
bool CompatableTest(int nStatusA, int nStatusB)
{
return !(nStatusA & nStatusB);
}
bool CompatableTest( int nStatusA, int nStatuB, int nStatusC)
{
return CompatableTest(nStatusA, nStatuB) && CompatableTest(nStatusA, nStatusC) && CompatableTest(nStatuB, nStatusC);
}
int main()
{
int i,j,k,m;
int nRow, nCol;
char c;
int nStatusAccount;
while(scanf("%d%d", &nRow, &nCol) != EOF)
{
if(nRow == 0 && nCol == 0)
break;
nStatusAccount = GetAllLegalStatus(nCol);
memset(g_DP, -1, sizeof(g_DP));
for( i = 1; i <= nRow; i++)
{
getchar();
int hilly = 0;
for( j = 0; j < nCol; j++)
{
hilly <<= 1;
c = getchar();
if( c == 'H')
{
hilly += 1;
}
}
g_Hilly[i] = hilly;
}
for( j = 1; j <= nStatusAccount; j++)
{
if(TestIsLegalStatus(g_LegalStatus[j], 1))
{
g_DP[1][1][j] = g_nGunForStatus[j];
}
}
for( i = 2; i <= nRow; i++)
{
for( j = 1; j <= nStatusAccount; j++) //test for line i
{
if(TestIsLegalStatus(g_LegalStatus[j], i))
{
for( k = 1; k <= nStatusAccount; k++) //test for line i-1
{
if(CompatableTest(g_LegalStatus[j], g_LegalStatus[k]))
{
for(m = 1; m <= nStatusAccount; m++) //test for line i-2
{
if( g_DP[i-1][m][k] != -1
&& CompatableTest(g_LegalStatus[j], g_LegalStatus[m], g_LegalStatus[k]))
{
g_DP[i][k][j] = max((g_DP[i-1][m][k] + g_nGunForStatus[j]), g_DP[i][k][j] );
}
}
}
}
}
}
}
int maxPlacement = 0;
for( i = 1; i <= nRow; i++)
{
for( j = 1; j <= nStatusAccount; j++)
{
for( k = 1; k <= nStatusAccount; k++)
{
maxPlacement = max(maxPlacement, g_DP[i][k][j]);
}
}
}
printf("%d\n", maxPlacement);
}
}
纠结:判断三个时候冲突那段代码我debug了一个上午,最后发现居然位运算理解错了,
s1, s2, s3
我弄成 if(s1 & s2 & s3) return false
可是呢,其实只要有任意两个 与运算的值非 0,就应该 return false;