C语言版的线性回归分析函数

        前几天，清理出一些十年以前 DOS 下的程序及代码，看来目前也没什么用了，想打个包刻在光碟上，却发现有些代码现在可能还能起作用，其中就有计算一元回归和多元回归的代码，一看代码文件时间，居然是 1993 年的，于是稍作整理，存放在这，分析虽不十分完整，但一般应用是没问题的，最起码，可提供给那些刚学 C 的学生们参考。

先看看一元线性回归函数代码： 

//  求线性回归方程：Y = a + bx
//  dada[rows*2]数组：X, Y；rows：数据行数；a, b：返回回归系数
//  SquarePoor[4]：返回方差分析指标: 回归平方和，剩余平方和，回归平方差，剩余平方差
//  返回值：0求解成功，-1错误
int  LinearRegression( double   * data,  int  rows,  double   * a,  double   * b,  double   * SquarePoor)
{
     int  m;
     double   * p, Lxx  =   0.0 , Lxy  =   0.0 , xa  =   0.0 , ya  =   0.0 ;
     if  (data  ==   0   ||  a  ==   0   ||  b  ==   0   ||  rows  <   1 )
         return   - 1 ;
     for  (p  =  data, m  =   0 ; m  <  rows; m  ++ )
    {
        xa  +=   * p  ++ ;
        ya  +=   * p  ++ ;
    }
    xa  /=  rows;                                      //  X平均值
    ya  /=  rows;                                      //  Y平均值
     for  (p  =  data, m  =   0 ; m  <  rows; m  ++ , p  +=   2 )
    {
        Lxx  +=  (( * p  -  xa)  *  ( * p  -  xa));              //  Lxx = Sum((X - Xa)平方)
        Lxy  +=  (( * p  -  xa)  *  ( * (p  +   1 )  -  ya));        //  Lxy = Sum((X - Xa)(Y - Ya))
    }
     * b  =  Lxy  /  Lxx;                                  //  b = Lxy / Lxx
     * a  =  ya  -   * b  *  xa;                               //  a = Ya - b*Xa
     if  (SquarePoor  ==   0 )
         return   0 ;
     //  方差分析
    SquarePoor[ 0 ]  =  SquarePoor[ 1 ]  =   0.0 ;
     for  (p  =  data, m  =   0 ; m  <  rows; m  ++ , p  ++ )
    {
        Lxy  =   * a  +   * b  *   * p  ++ ;
        SquarePoor[ 0 ]  +=  ((Lxy  -  ya)  *  (Lxy  -  ya));  //  U(回归平方和)
        SquarePoor[ 1 ]  +=  (( * p  -  Lxy)  *  ( * p  -  Lxy));  //  Q(剩余平方和)
    }
    SquarePoor[ 2 ]  =  SquarePoor[ 0 ];                   //  回归方差
    SquarePoor[ 3 ]  =  SquarePoor[ 1 ]  /  (rows  -   2 );      //  剩余方差
     return   0 ;
}

 

为了理解代码，把几个与代码有关的公式写在下面（回归理论和公式推导就免了，网上搜索到处是，下面的公式图片也是网上搜的，有些公式图形网上没找到或者不合适，可参见后面多元回归中的公式）：

1、回归方程式：

2、回归系数：   

   其中：

         

          

3、回归平方和：

4、剩余平方和：

实例计算：

double  data1[ 12 ][ 2 ]  =  {
//     X      Y
    { 187.1 ,  25.4 },
    { 179.5 ,  22.8 },
    { 157.0 ,  20.6 },
    { 197.0 ,  21.8 },
    { 239.4 ,  32.4 },
    { 217.8 ,  24.4 },
    { 227.1 ,  29.3 },
    { 233.4 ,  27.9 },
    { 242.0 ,  27.8 },
    { 251.9 ,  34.2 },
    { 230.0 ,  29.2 },
    { 271.8 ,  30.0 }
};

void  Display( double   * dat,  double   * Answer,  double   * SquarePoor,  int  rows,  int  cols)
{
     double  v,  * p;
     int  i, j;
    printf( " 回归方程式:    Y = %.5lf " , Answer[ 0 ]);
     for  (i  =   1 ; i  <  cols; i  ++ )
        printf( "  + %.5lf*X%d " , Answer[i], i);
    printf( " " );
    printf( " 回归显著性检验: " );
    printf( " 回归平方和：%12.4lf  回归方差：%12.4lf " , SquarePoor[ 0 ], SquarePoor[ 2 ]);
    printf( " 剩余平方和：%12.4lf  剩余方差：%12.4lf " , SquarePoor[ 1 ], SquarePoor[ 3 ]);
    printf( " 离差平方和：%12.4lf  标准误差：%12.4lf " , SquarePoor[ 0 ]  +  SquarePoor[ 1 ], sqrt(SquarePoor[ 3 ]));
    printf( " F   检  验：%12.4lf  相关系数：%12.4lf " , SquarePoor[ 2 ]  / SquarePoor[ 3 ],
           sqrt(SquarePoor[ 0 ]  /  (SquarePoor[ 0 ]  +  SquarePoor[ 1 ])));
    printf( " 剩余分析: " );
    printf( "       观察值      估计值      剩余值    剩余平方 " );
     for  (i  =   0 , p  =  dat; i  <  rows; i  ++ , p  ++ )
    {
        v  =  Answer[ 0 ];
         for  (j  =   1 ; j  <  cols; j  ++ , p  ++ )
            v  +=   * p  *  Answer[j];
        printf( " %12.2lf%12.2lf%12.2lf%12.2lf " ,  * p, v,  * p  -  v, ( * p  -  v)  *  ( * p  -  v));
    }
    system( " pause " );
}

int  main()
{
     double  Answer[2 ], SquarePoor[ 4 ];
     if  (LinearRegression(( double * )data1,  12 ,  & Answer[ 0 ],  & Answer[ 1 ], SquarePoor)  ==   0 )
        Display(( double * )data1, Answer, SquarePoor,  12 ,  2 );
     return   0 ;
}

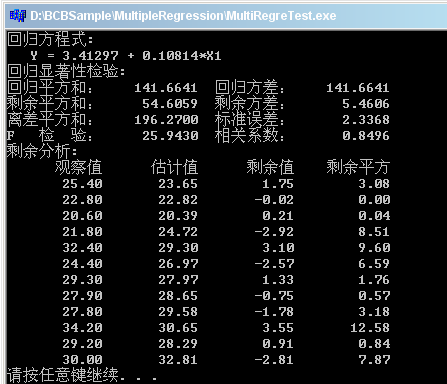
    运行结果：

 

上面的函数和例子程序不仅计算了回归方程式，还计算了显著性检验指标，例如F检验指标，我们可以在统计F分布表上查到F0.01(1,10)=10.04（注：括号里的1,10分别为回归平方和和剩余平方和所拥有的自由度），小于计算的F检验值25.94，可以认为该回归例子高度显著。

如果使用图形界面，可以根据原始数据和计算结果绘制各种图表，如散点图、趋势图、控制图等。很多非线性方程可以借助数学计算，转化为直线方程进行回归分析。

同一元线性回归相比，多元线性回归分析代码可就复杂多了，必须求解线性方程，因此本代码中包含一个可独立使用的线性方程求解函数：

 

void  FreeData( double   ** dat,  double   * d,  int  count)
{
     int  i, j;
    free(d);
     for  (i  =   0 ; i  <  count; i  ++ )
        free(dat[i]);
    free(dat);
}
//  解线性方程。data[count*(count+1)]矩阵数组；count：方程元数；
//  Answer[count]：求解数组 。返回：0求解成功，-1无解或者无穷解
int  LinearEquations( double   * data,  int  count,  double   * Answer)
{
     int  j, m, n;
     double  tmp,  ** dat,  * d  =  data;
    dat  =  ( double ** )malloc(count  *   sizeof ( double * ));
     for  (m  =   0 ; m  <  count; m  ++ , d  +=  (count  +   1 ))
    {
        dat[m]  =  ( double * )malloc((count  +   1 )  *   sizeof ( double ));
        memcpy(dat[m], d, (count  +   1 )  *   sizeof ( double ));
    }
    d  =  ( double * )malloc((count  +   1 )  *   sizeof ( double ));
     for  (m  =   0 ; m  <  count  -   1 ; m  ++ )
    {
         //  如果主对角线元素为0，行交换
         for  (n  =  m  +   1 ; n  <  count  &&  dat[m][m]  ==   0.0 ; n  ++ )
        {
             if  ( dat[n][m]  !=   0.0 )
            {
                memcpy(d, dat[m], (count  +   1 )  *   sizeof ( double ));
                memcpy(dat[m], dat[n], (count  +   1 )  *   sizeof ( double ));
                memcpy(dat[n], d, (count  +   1 )  *   sizeof ( double ));
            }
        }
         //  行交换后，主对角线元素仍然为0，无解，返回-1
         if  (dat[m][m]  ==   0.0 )
        {
            FreeData(dat, d, count);
             return   - 1 ;
        }
         //  消元
         for  (n  =  m  +   1 ; n  <  count; n  ++ )
        {
            tmp  =  dat[n][m]  /  dat[m][m];
             for  (j  =  m; j  <=  count; j  ++ )
                dat[n][j]  -=  tmp  *  dat[m][j];
        }
    }
     for  (j  =   0 ; j  <  count; j  ++ )
        d[j]  =   0.0 ;
     //  求得count - 1的元
    Answer[count  -   1 ]  =  dat[count  -   1 ][count]  /  dat[count  -   1 ][count  -   1 ];
     //  逐行代入求各元
     for  (m  =  count  -   2 ; m  >=   0 ; m  -- )
    {
         for  (j  =  count  -   1 ; j  >  m; j  -- )
            d[m]  +=  Answer[j]  *  dat[m][j];
        Answer[m]  =  (dat[m][count]  -  d[m])  /  dat[m][m];
    }
    FreeData(dat, d, count);
     return   0 ;
}

//  求多元回归方程：Y = B0 + B1X1 + B2X2 + ...BnXn
//  data[rows*cols]二维数组；X1i,X2i,...Xni,Yi (i=0 to rows-1)
//  rows：数据行数；cols数据列数；Answer[cols]：返回回归系数数组(B0,B1...Bn)
//  SquarePoor[4]：返回方差分析指标: 回归平方和，剩余平方和，回归平方差，剩余平方差
//  返回值：0求解成功，-1错误
int  MultipleRegression( double   * data,  int  rows,  int  cols,  double   * Answer,  double   * SquarePoor)
{
     int  m, n, i, count  =  cols  -   1 ;
     double   * dat,  * p, a, b;
     if  (data  ==   0   ||  Answer  ==   0   ||  rows  <   2   ||  cols  <   2 )
         return   - 1 ;
    dat  =  ( double * )malloc(cols  *  (cols  +   1 )  *   sizeof ( double ));
    dat[ 0 ]  =  ( double )rows;
     for  (n  =   0 ; n  <  count; n  ++ )                      //  n = 0 to cols - 2
    {
        a  =  b  =   0.0 ;
         for  (p  =  data  +  n, m  =   0 ; m  <  rows; m  ++ , p  +=  cols)
        {
            a  +=   * p;
            b  +=  ( * p  *   * p);
        }
        dat[n  +   1 ]  =  a;                               //  dat[0, n+1] = Sum(Xn)
        dat[(n  +   1 )  *  (cols  +   1 )]  =  a;                //  dat[n+1, 0] = Sum(Xn)
        dat[(n  +   1 )  *  (cols  +   1 )  +  n  +   1 ]  =  b;        //  dat[n+1,n+1] = Sum(Xn * Xn)
         for  (i  =  n  +   1 ; i  <  count; i  ++ )              //  i = n+1 to cols - 2
        {
             for  (a  =   0.0 , p  =  data, m  =   0 ; m  <  rows; m  ++ , p  +=  cols)
                a  +=  (p[n]  *  p[i]);
            dat[(n  +   1 )  *  (cols  +   1 )  +  i  +   1 ]  =  a;    //  dat[n+1, i+1] = Sum(Xn * Xi)
            dat[(i  +   1 )  *  (cols  +   1 )  +  n  +   1 ]  =  a;    //  dat[i+1, n+1] = Sum(Xn * Xi)
        }
    }
     for  (b  =   0.0 , m  =   0 , p  =  data  +  n; m  <  rows; m  ++ , p  +=  cols)
        b  +=   * p;
    dat[cols]  =  b;                                    //  dat[0, cols] = Sum(Y)
     for  (n  =   0 ; n  <  count; n  ++ )
    {
         for  (a  =   0.0 , p  =  data, m  =   0 ; m  <  rows; m  ++ , p  +=  cols)
            a  +=  (p[n]  *  p[count]);
        dat[(n  +   1 )  *  (cols  +   1 )  +  cols]  =  a;         //  dat[n+1, cols] = Sum(Xn * Y)
    }
    n  =  LinearEquations(dat, cols, Answer);           //  计算方程式
     //  方差分析
     if  (n  ==   0   &&  SquarePoor)
    {
        b  =  b  /  rows;                                 //  b = Y的平均值
        SquarePoor[ 0 ]  =  SquarePoor[ 1 ]  =   0.0 ;
        p  =  data;
         for  (m  =   0 ; m  <  rows; m  ++ , p  ++ )
        {
             for  (i  =   1 , a  =  Answer[ 0 ]; i  <  cols; i  ++ , p  ++ )
                a  +=  ( * p  *  Answer[i]);                //  a = Ym的估计值
            SquarePoor[ 0 ]  +=  ((a  -  b)  *  (a  -  b));     //  U(回归平方和)
            SquarePoor[ 1 ]  +=  (( * p  -  a)  *  ( * p  -  a));   //  Q(剩余平方和)(*p = Ym)
        }
        SquarePoor[ 2 ]  =  SquarePoor[ 0 ]  /  count;        //  回归方差

  if (rows - cols > 0.0)
    SquarePoor[3] = SquarePoor[1] / (rows - cols); // 剩余方差
  else
    SquarePoor[3] = 0.0;

    }
    free(dat);
     return  n;
}

为了理解代码，同样贴几个主要公式在下面，其中回归平方和和剩余平方和公式和一元回归相同：

1、回归方程式：,

2、回归系数方程组：

　　　　

3、F检验：

4、相关系数：，其中，Syy是离差平方和（回归平方和与剩余平方和之和）。该公式其实就是U/(U+Q)的平方根（没找到这个公式的图）。

5、回归方差：U / m，m为回归方程式中自变量的个数（没找到图）。

6、剩余方差：Q / (n - m - 1)，n为观察数据的样本数，m同上（没找到图）。

7、标准误差：也叫标准误，就是剩余方差的平方根（没找到图）。

下面是一个多元回归的例子：

double  data[ 15 ][ 5 ]  =  {
//    X1   X2    X3   X4    Y
  {  316 ,  1536 ,  874 ,  981 ,  3894  },
  {  385 ,  1771 ,  777 ,  1386 ,  4628  },
  {  299 ,  1565 ,  678 ,  1672 ,  4569  },
  {  326 ,  1970 ,  785 ,  1864 ,  5340  },
  {  441 ,  1890 ,  785 ,  2143 ,  5449  },
  {  460 ,  2050 ,  709 ,  2176 ,  5599  },
  {  470 ,  1873 ,  673 ,  1769 ,  5010  },
  {  504 ,  1955 ,  793 ,  2207 ,  5694  },
  {  348 ,  2016 ,  968 ,  2251 ,  5792  },
  {  400 ,  2199 ,  944 ,  2390 ,  6126  },
  {  496 ,  1328 ,  749 ,  2287 ,  5025  },
  {  497 ,  1920 ,  952 ,  2388 ,  5924  },
  {  533 ,  1400 ,  1452 ,  2093 ,  5657  },
  {  506 ,  1612 ,  1587 ,  2083 ,  6019  },
  {  458 ,  1613 ,  1485 ,  2390 ,  6141  },
};

void  Display( double   * dat,  double   * Answer,  double   * SquarePoor,  int  rows,  int  cols)
{
     double  v,  * p;
     int  i, j;
    printf( " 回归方程式:    Y = %.5lf " , Answer[ 0 ]);
     for  (i  =   1 ; i  <  cols; i  ++ )
        printf( "  + %.5lf*X%d " , Answer[i], i);
    printf( " " );
    printf( " 回归显著性检验: " );
    printf( " 回归平方和：%12.4lf  回归方差：%12.4lf " , SquarePoor[ 0 ], SquarePoor[ 2 ]);
    printf( " 剩余平方和：%12.4lf  剩余方差：%12.4lf " , SquarePoor[ 1 ], SquarePoor[ 3 ]);
    printf( " 离差平方和：%12.4lf  标准误差：%12.4lf " , SquarePoor[ 0 ]  +  SquarePoor[ 1 ], sqrt(SquarePoor[ 3 ]));
    printf( " F   检  验：%12.4lf  相关系数：%12.4lf " , SquarePoor[ 2 ]  /  SquarePoor[ 3 ],
           sqrt(SquarePoor[ 0 ]  /  (SquarePoor[ 0 ]  +  SquarePoor[ 1 ])));
    printf( " 剩余分析: " );
    printf( "       观察值      估计值      剩余值    剩余平方 " );
     for  (i  =   0 , p  =  dat; i  <  rows; i  ++ , p  ++ )
    {
        v  =  Answer[ 0 ];
         for  (j  =   1 ; j  <  cols; j  ++ , p  ++ )
            v  +=   * p  *  Answer[j];
        printf( " %12.2lf%12.2lf%12.2lf%12.2lf " ,  * p, v,  * p  -  v, ( * p  -  v)  *  ( * p  -  v));
    }
    system( " pause " );
}

int  main()
{
     double  Answer[ 5 ], SquarePoor[ 4 ];
     if  (MultipleRegression(( double * )data,  15 ,  5 , Answer, SquarePoor)  ==   0 )
        Display(( double * )data, Answer, SquarePoor,  15 ,  5 );
     return   0 ;
}

    运行结果见下图，同上面，查F分布表，F检验远远大于F0.005(4,10)的7.34，可以说是极度回归显著。

如果要根据回归方程进行预测和控制，还应该计算很多指标，如偏相关指标，t分布检验指标等，不过，本文只是介绍2个函数，并不是完整的回归分析程序，因此没必要计算那些指标。

其实，一元线性回归是多元线性回归的一个特例，完全可以使用同一个函数，如前面的例子：

if (MultipleRegression((double*)data1, 12, 2, Answer, SquarePoor) == 0)
        Display((double*)data, Answer, SquarePoor, 12, 2);

其运行结果是一样的，可能以前我为了DOS下的运行速度，单独写了一个函数，因为毕竟多元回归分析很少用到，而一元回归是经常使用的。

本文到此就该结束了，本来只是介绍以前的几个C函数，却介绍起统计知识来了，不过，如果谁想使用这些函数，完全不懂有关知识是不行的，相信大多数人应该能够看懂，毕竟大学生以上学历的人居多，比我的水平高多了。什么？你问我懂不懂？呵呵，不瞒你说，我的主业就是统计，而且统计师职务已经有20年，也就是文革后第一批评定的，而且第一批全国自学考试统计大专毕业，编程序只是我的业余爱好，不过我退养休息了近10年，也忘得差不多了，但是还是能看懂这些简单的东东。

补记：应一些朋友要求，《Delphi版的线性回归分析》已经发布。（2007.11.26）