【算法分析与设计】——八皇后问题的详解

    八皇后问题是一个以国际象棋为背景的问题：如何能够在 8×8 的国际象棋棋盘上放置八个皇后，使得任何一个皇后都无法直接吃掉其他的皇后？为了达到此目的，任两个皇后都不能处于同一条横行、纵行或斜线上。八皇后问题可以推广为更一般的n皇后摆放问题：这时棋盘的大小变为n×n，而皇后个数也变成n。

    这个问题简化描述就是：在8x8的棋盘上放8颗子，要求它们【不在同一行】【不在同一列】【不在同一斜线】上。面对问题，我们的思维要清晰：

第一，我们怎么用数据表示棋盘【数据表示】；

第二，我们用什么思路解决问题【解题策略】；

第三，我们怎么实现最后的代码【代码实现】。

【数据表示】：

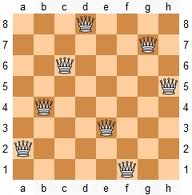
    这个问题的最简单数据表示方式，是用长度为8的一维数组，比如arr[8]={3,6,2,7,1,4,0,5}表示的就是上图的棋盘，arr[0]==3表示第0行（计算机中习惯从0开始）的皇后放在第3列（d列），arr[1]==6表示第1行的皇后放在第6列（g列）

【解题策略】

1.【穷举法】是不现实的，因为哪怕只是8x8的棋盘，所有解就包括 [00000000] 到 [77777777] ，共有16777216个解。

2.【分治法】是低效的，因为分治法一般相当于遍历树型解空间的所有枝叶，在此题中其实相当于穷举法。

3.【回溯发】是最佳策略，回溯和分治十分相似，但回溯不会遍历整个解空间，在遍历过程中有剪枝步骤。

【代码实现】

const int num  = 8;/*可以随意修改，num是多少解的就是几皇后问题*/
      int arr[num];
      int count =0;
void display()/*一个简单的数组输出函数，顺便统计解的个数*/
{
	for(int i=0; i<num; ++i)
		printf("%d\t",arr[i]);
	printf("\n");
	count++;
}

void queens(int pos=0)
{		
	/*剪枝步骤*/
	/*同在斜线或者直线上*/
	for(int i=0; i<pos-1; ++i)
	{
		int off = arr[i] - arr[pos-1];
		if(off ==0 || off ==pos-1-i || -off==pos-1-i)
			return;
	}

	/*符合条件就输出*/
	if( pos == num )
	{	display();return;}
	
	
	/*递归搜索解空间*/
	for(int k=0; k<num; ++k)
	{
		arr[pos]=k;
		queens(pos+1);
	}
}

测试代码如下：

void main(int i,int j)
{
	queens();
	printf("count:%d",count);
	getchar();
}

代码由三部分组成

function
   begin
       检查上一步是否正确【剪枝】
       如果满足条件就输出【输出】
       递归下一步的可能值【递归】   
   end

这就像你自己下棋：

1.每次都检查上一步的局势，如果已经输了就结束这一盘的【剪枝】，后面我再怎么落子都是白搭（穷举法则会继续走）,这盘咱们不玩儿了，。

2.如果还没有输，那么是不是应经赢了，如果应经赢了，这盘咱们结束了【输出】，再来新的一盘。

3.如果还在焦灼状态，杀得难分难解，那么我继续落子【递归】，直到“我输”或者“我赢”。

回溯法是不是有种“弈棋之道”的感觉？