EM模型测试用例
作者:金良([email protected]) csdn博客: http://blog.csdn.net/u012176591
1.em4gmm
em4gmm is a toolkit to work with Finite Gaussian Mixture Models. In fact, it is a very fast and parallel C implementation of the clustering Expectation Maximization (EM) algorithm for estimating Gaussian Mixture Models (GMMs), with some extra important improvements. This is a full list of features that this toolkit contains:
- Fast learning of Gaussian Mixture Models (GMMs) using multidimensional data.
- Fast merge similar components to simplify the learned Gaussian Mixture Model.
- Fast simple classification score for a group of data (the data can be compressed).
- Obtain a detailed classification for each sample of a group of data (auto-clustering).
- Use a World Model to normalize classification scores (for biometric tasks).
- Possibility of set the number of threads to use on the execution of any task.
- Extra tool used to generate random synthetic data files, for any purpose.
地址https://github.com/juandavm/em4gmm
下载后的文件目录

其中bin/datagen.py 是个Python脚本用来生成指定维度和样本数的数据,用于训练或测试。比如生成5000个2维数据并保存成文本文件data.txt,命令如下:

data/data.gz 是一个压缩的数据文件,内容是10000个10维的样本数据。
用make 命令编译后在bin目录下生成训练用的可执行文件 gmmtrain 和测试用的可执行文件 gmmclass。
直接用编译后生成的gmmtrain 训练程序自带的数据data/data.gz,如下:
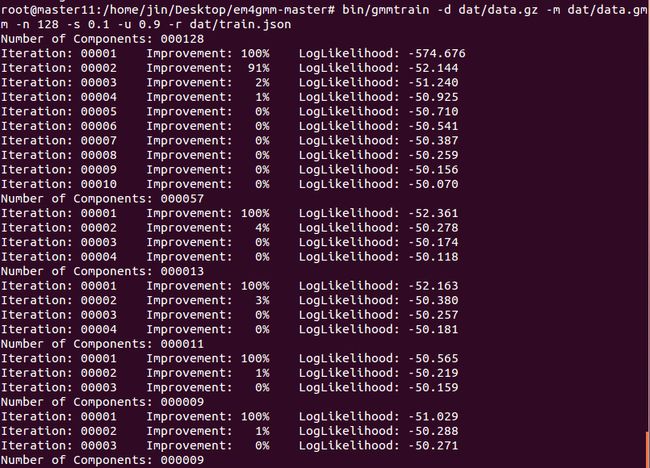
命令和参数设置是
bin/gmmtrain -d dat/data.gz -m dat/data.gmm -n 128 -s 0.1 -u 0.9 -r dat/train.json
-d dat/data.gz 表示训练数据;
-m dat/data.gmm 表示存储训练模型的地址,测试时用到该文件。
-n 128 表示初始的类的数目的设置;
-s 0.1 基于似然函数的停止训练的标准;
-u 0.9 合并相近的类别的门限值,自动缩减到合适的类的数目。
-r dat/train.json 存储最终确定的各个类的参数,包括中心位置,协方差矩阵等。
下面是dat/train.json的内容,可以看到起协方差矩阵只给出了对角元素,所以设定的协方差矩阵是对角阵:
{
“dimension”: 10,
“classes”: 9,
“minimum_dcov”: [ 0.0664811718, 0.0665756705, 0.0661713018, 0.0663868848, 0.0663586954, 0.0663599001, 0.0663704719, 0.0665865695, 0.0663445058, 0.0661974397 ],
“model”: [
{ “class”: 0, “lprior”: -2.1015089647, “means”: [ 281.1754542697, 281.6401497588, 280.8204018065, 281.3086966233, 281.4134791472, 281.7143823581, 281.3546990321, 281.7972527764, 281.1608653803, 281.1348176896 ], “dcov”: [ 1104.2276141386, 1085.7272861633, 1094.7559483724, 1108.9310900716, 1088.8696166679, 1080.7311641372, 1092.5478736575, 1113.6949102885, 1093.8579627279, 1096.9961977462 ] },
用生成的模型预测训练数据所属的聚簇,命令如下:
bin/gmmclass -d dat/data.gz -m dat/data.gmm -r dat/class.json
参数-d dat/data.gz表示预测的数据,dat/data.gmm 表示模型,-r dat/class.json 表示预测的聚簇结果。
-r dat/class.json 前几行内容如下
{
“samples”: 100000,
“classes”: 9,
“samples_results”: [
{ “sample”: 0, “lprob”: [ -293.0498043941, -69.8653772127, -233.4779265982, -94.1832783176, -59.8669282879, -52.8054070815, -193.7279876227, -99.9986598253, -248.8566776327 ], “class”: 5 },
{ “sample”: 1, “lprob”: [ -302.5703483327, -81.8610237579, -243.6801703783, -102.0671109962, -79.1293826982, -66.6184285099, -233.3150272424, -160.3292125728, -271.5707084665 ], “class”: 5 },
sample0 属于各个聚簇的概率值用列表已经列出,可以看到第5个值-52.8054070815 是最大的,所以sample0 被划分到簇class5。
为了作可视化分析,用开头产生的5000个2维数据进行分类,最终得到8个类别。如下图,其中同类用同一种颜色表示,点表示样本,方框表示类的中心点。
效果还是不错的,呵呵。
聚类效果图代码:
import json
import numpy as np
import matplotlib.pyplot as plt
def probcomputing(XX,traindata):
ZZ = np.zeros(XX.shape[0])
i = 0
for xy in XX: #对每一个坐标点
if i%10000 ==0: #监控程序进度
print i
for gauss in traindata: #对每一个高斯函数
deltas = np.array([gauss['dcov'] [0],gauss['dcov'][1]]) #该高斯函数的方差,注意非标准差
means = np.array([gauss['means'][0],gauss['means'][1]]) #高斯函数的中心
deltaprod = gauss['dcov'][0]*gauss['dcov'][1]
ZZ[i] += 1.0/np.product(np.power(deltas,0.5))*np.exp(-sum(np.power(xy-means,2)/deltas)*1.0/2) #加上坐标点xy在该高斯函数处的概率
i = i+1
return ZZ
#解析测试产生的分类文件
with open("class.json", "r") as f:
classdata = json.load(f)
classdata = classdata['samples_results']
#解析训练产生的模型文件
with open("train.json", "r") as f:
traindata = json.load(f)
traindata = traindata['model']
#解析原始数据文件
data = []
for line in open("data.txt"):
temp = map(float,line.split(' '))
data.append([temp[0],temp[1]])
del data[0]
x = np.linspace(-10000.0,10000.0,1000)
y = np.linspace(-10000.0,10000.0,1000)
X, Y = np.meshgrid(x, y)
XX = np.array([X.ravel(), Y.ravel()]).T
Z = probcomputing(XX,traindata)
Z = Z.reshape(X.shape)
plt.contour(X,Y,Z) #作概率的等高线
#一共8个类,用8种颜色
color = ['b','g','r','c','m','y','k','w']
for i in range(len(data)):#画每个数据点
cls = classdata[i]['class'] #该点所属类
colr = color[cls] #该点的颜色
plt.plot(data[i][0],data[i][1],'.'+colr)
for i in range(len(traindata)):#对每个聚簇中心
cls = traindata[i]['class'] #该中心对应的类
colr = color[cls] #该中心点的颜色
plt.plot(traindata[i]['means'][0],traindata[i]['means'][1],'s'+colr,markersize = 10)
#给该聚类中心编号
plt.annotate('%s)' %cls, xy=(traindata[i]['means'][0],traindata[i]['means'][1]), xytext=(10,0), textcoords='offset points')
plt.xlabel(u'X坐标',{'fontname':'STKaiti'})
plt.ylabel(u'Y坐标',{'fontname':'STKaiti'})
plt.title(u'GMM模型聚类效果图',{'fontname':'STKaiti'})代码中的文件data.txt 前几行内容:
2 5000
2617.165 9381.795
-5457.983 -2983.188
926.058 5096.768
888.685 -9876.404
-3301.636 4774.197
-3500.600 -2034.212
380.454 -9755.139
5398.821 -1393.021
-9557.110 -8500.632
1108.280 5082.505
9764.796 4278.778
-3618.278 -1941.091
-7230.196 7047.653
文件 train.json 的内容:
{
“dimension”: 2,
“classes”: 8,
“minimum_dcov”: [ 254.7205181165, 296.9317178374 ],
“model”: [
{ “class”: 0, “lprior”: -2.9931390552, “means”: [ -7377.0296207224, -7773.1160129017 ], “dcov”: [ 7027506.0895558670, 869811.8710054532 ] },
{ “class”: 1, “lprior”: -2.8025953304, “means”: [ 2932.7678383148, 3204.6842125823 ], “dcov”: [ 4152473.7082074001, 21102790.6513020024 ] },
{ “class”: 2, “lprior”: -1.3957920051, “means”: [ 886.6602869926, -8951.6361159455 ], “dcov”: [ 13412365.2566275094, 741705.8073216379 ] },
{ “class”: 3, “lprior”: -1.6784763753, “means”: [ -3137.7102188004, 6754.2708985954 ], “dcov”: [ 12148375.4655964877, 2107581.7905958742 ] },
{ “class”: 4, “lprior”: -2.9551400195, “means”: [ -8919.8592857451, -2624.8307833796 ], “dcov”: [ 646940.8650369942, 11770608.8125911355 ] },
{ “class”: 5, “lprior”: -2.6114430738, “means”: [ 3593.3589274772, -5364.2969417472 ], “dcov”: [ 691482.6675975025, 204528.3210635446 ] },
{ “class”: 6, “lprior”: -2.3373524608, “means”: [ -5412.7781222819, -3397.3109982231 ], “dcov”: [ 1590086.4328696877, 1236343.7897034772 ] },
{ “class”: 7, “lprior”: -1.4574043607, “means”: [ 7135.2130309072, -672.3724348074 ], “dcov”: [ 5412506.6176119149, 18685779.8571773283 ] }
]
}
文件 class.json 前几行内容
{
“samples”: 5000,
“classes”: 8,
“samples_results”: [
{ “sample”: 0, “lprob”: [ -195.8276681423, -21.6085987653, -244.8917241597, -21.9541878009, -128.6182848211, -549.5581084700, -104.6480825182, -24.0096310521 ], “class”: 1 },
{ “sample”: 1, “lprob”: [ -33.0024466664, -30.0771988190, -43.7123311742, -41.6693377652, -28.8915414817, -90.3871711693, -18.3987129401, -34.2121133426 ], “class”: 6 },
{ “sample”: 2, “lprob”: [ -119.6692988117, -21.2622379402, -151.2410101742, -20.2846901121, -97.0797438782, -289.9586724840, -60.1420376937, -23.8711557767 ], “class”: 3 },
{ “sample”: 3, “lprob”: [ -26.9557232414, -25.2499629046, -18.7743729746, -85.2358057932, -96.2130811298, -72.3472779337, -47.7918956566, -25.2903713263 ], “class”: 2 },
{ “sample”: 4, “lprob”: [ -111.2328966369, -25.4309804404, -145.8553278444, -19.8844784068, -46.3442473242, -302.9461415963, -46.7346246587, -30.2754218073 ], “class”: 3 },
{ “sample”: 5, “lprob”: [ -39.5531044530, -26.3263938168, -51.1726502047, -37.2823615535, -42.3362773348, -80.7853598550, -20.2298950856, -29.9185753812 ], “class”: 6 },
{ “sample”: 6, “lprob”: [ -26.0915451542, -25.4564240918, -18.6426437880, -84.1245924038, -88.6331230706, -71.8826679628, -45.2294681489, -25.8414398394 ], “class”: 2 },
2.JMEF
A Java library to create, process and manage mixtures of exponential families
在eclipse工程目录如下:

Tutorials目录下是5个例子。
没仔细研究。
3.A specializer for Gaussian Mixture Models, based on the ASP framework
用Python写的,相关论文《CUDA-level Performance with Python-level Productivity for Gaussian Mixture Model Applications》和《Fast speaker diarization using a high-level scripting language》,里面有一个语音的数据(样本数是158265,维度是19),配置环境比较复杂。
github源码地址https://github.com/hcook/gmm
github上的说明文档地址https://github.com/hcook/gmm/wiki/Using-the-GMM-Specializer
这里汇合了相关的东西,下载地址http://download.csdn.net/detail/u012176591/8680025


