用UFLDL的方法改写Denoising Autoencoder

最近在学Autoencoder的相关知识，已经学习完DFLDL的Sparse_Autoencoder相关知识，想学学Denoising Autoencoder和contractive Autoencoder。

本篇先说说Denoising Autoencoder的学习。

参考大神tornadomeet的博客（http://www.cnblogs.com/tornadomeet/p/3261247.html），我准备自己尝试第一个实验。下载完DeepLearnToolbox并且自己把代码test_example_SAE跑了一遍后发现，没有Denoising时候，识别结果error为0.10，然后加上50%的Denoising后，就出现“Too big error”的警告，原来是识别结果error超过0.16，而代码的最后一句为

assert(er < 0.16, 'Too big error')。

但是tornadomeet大神不是说加上50%的Denoising后test的结果会更好吗？仔细对比了一下发现，toolbox里面的代码网络结构是[784 100 10]的，也就是只有一层hidden layer，代码如下：

function test_example_SAE
load ../data/mnist_uint8;

train_x = double(train_x)/255;
test_x  = double(test_x)/255;
train_y = double(train_y);
test_y  = double(test_y);

addpath('../SAE')
addpath('../NN')

%%  ex1 train a 100 hidden unit SDAE and use it to initialize a FFNN
%  Setup and train a stacked denoising autoencoder (SDAE)
rand('state',0)
sae = saesetup([784 100]);
sae.ae{1}.activation_function       = 'sigm';
sae.ae{1}.learningRate              = 1;
sae.ae{1}.inputZeroMaskedFraction   = 0.5;
opts.numepochs =   1;
opts.batchsize = 100;
sae = saetrain(sae, train_x, opts);
visualize(sae.ae{1}.W{1}(:,2:end)')

% Use the SDAE to initialize a FFNN
nn = nnsetup([784 100 10]);
nn.activation_function              = 'sigm';
nn.learningRate                     = 1;
nn.W{1} = sae.ae{1}.W{1};

% Train the FFNN
opts.numepochs =   1;
opts.batchsize = 100;
nn = nntrain(nn, train_x, train_y, opts);
[er, bad] = nntest(nn, test_x, test_y);
assert(er < 0.16, 'Too big error');

而tornadomeet大神的代码是两层hidden layer，网络结构是[784 100 100 10]的，存在着这个差别，所以两层hidden layer的结果是：

接下来我自己尝试去写这整个代码，但是toolbox的代码由于是要适合多个test的，所以每个被调用的函数里面都列举了各种的可能性，

        switch nn.activation_function 
            case 'sigm'
                % Calculate the unit's outputs (including the bias term)
                nn.a{i} = sigm(nn.a{i - 1} * nn.W{i - 1}');
            case 'tanh_opt'
                nn.a{i} = tanh_opt(nn.a{i - 1} * nn.W{i - 1}');
        end
        
        %dropout
        if(nn.dropoutFraction > 0)
            if(nn.testing)
                nn.a{i} = nn.a{i}.*(1 - nn.dropoutFraction);
            else
                nn.dropOutMask{i} = (rand(size(nn.a{i}))>nn.dropoutFraction);
                nn.a{i} = nn.a{i}.*nn.dropOutMask{i};
            end
        end
        
        %calculate running exponential activations for use with sparsity
        if(nn.nonSparsityPenalty>0)
            nn.p{i} = 0.99 * nn.p{i} + 0.01 * mean(nn.a{i}, 1);
        end
        
        %Add the bias term
        nn.a{i} = [ones(m,1) nn.a{i}];
    end
    switch nn.output 
        case 'sigm'
            nn.a{n} = sigm(nn.a{n - 1} * nn.W{n - 1}');
        case 'linear'
            nn.a{n} = nn.a{n - 1} * nn.W{n - 1}';
        case 'softmax'
            nn.a{n} = nn.a{n - 1} * nn.W{n - 1}';
            nn.a{n} = exp(bsxfun(@minus, nn.a{n}, max(nn.a{n},[],2)));
            nn.a{n} = bsxfun(@rdivide, nn.a{n}, sum(nn.a{n}, 2)); 
    end

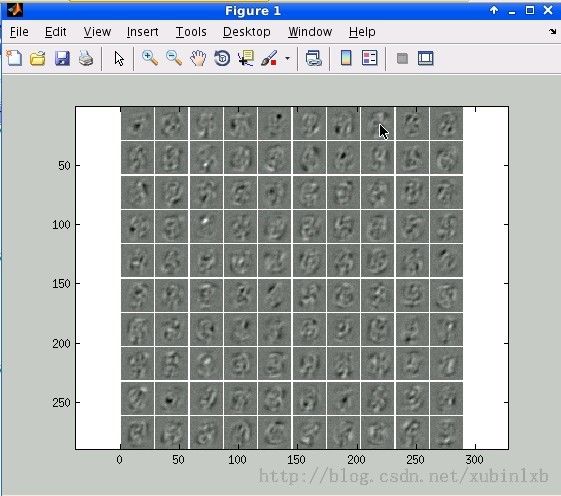
代码太冗余，不适合初学者，所以我自己尝试用UFLDL里面的那种代码风格，自己从头到尾写了一遍代码，结果发现，即使是用一层隐含层，网络结构是[784 100 10]，用了denoising后，效果也会比没有denoising好。

下面是自己写的代码和结果（本人是初学者，代码不够规范，希望大家见谅并批评指出）：

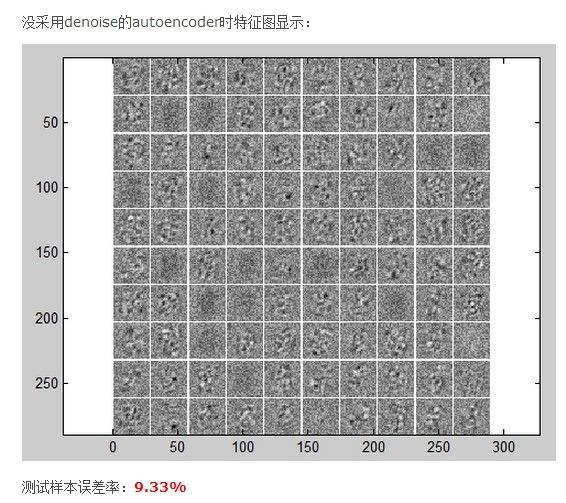
the error rate is 9.3%

加上denoising后，the error rate is 7.3%

%% Code for Denoising Autoencoder
% the network is [784 100 10]
% By xubinlxb

close all
clear
clc

%% load data
load './data/mnist_uint8.mat'
train_x = double(train_x'./255);
train_y = double(train_y');
test_x = double(test_x'./255);
test_y = double(test_y');

%% parameter initialized
nn = struct;
nn.visibleSize = size(train_x,1);
nn.hiddenSize = 100;
nn.outputSize = 10;
nn.lambda = 0.0001;
nn.batchSize=100;
nn.LearnRate = 3;
nn.Method = 'unsupervise';
nn.DenoisingPara = 0.5;

%% build Layer1 network

% configuration the cost funtion
rng('default');
nn = theta_initialization(nn);
disp('unsupervise train...')
[L1, nn] = batch_build(nn, train_x ,train_x);
[cost1,~] = build_one_layer_addWeight(nn,train_x,train_x);
 
% Visualization
visualize(nn.W1');
% display_network(nn.W1', 12);

%% train the whole network
nn.DenoisingPara = 0;
nn.Method = 'supervise';

W1 = nn.W1;
b1 = nn.b1;
nn = theta_initialization(nn);
nn.W1 = W1;
nn.b1 = b1;
clear W1 b1

disp('supervise train...')
[L2, nn] = batch_build(nn, train_x, train_y);
[cost2,~] = build_one_layer_addWeight(nn,train_x,train_y);

%% test the whole network
label = predict(nn,test_x);
[~,expected] = max(test_y,[],1);
badNum = numel(find(label~=expected));
er = badNum/size(test_y,2);
assert(er<0.16,'Too big error')
fprintf('the errror rate is %f\n',er)

function [ L, nn ] = batch_build( nn, train_x ,train_y)

m = size(train_x,2);
batchSize = nn.batchSize;
batchNum = m/ batchSize;
L = [];

for i = 1:batchNum
    
    if (mod(i,100) == 0)
        fprintf('batch %d,\n',i);
    end
    
    kk = randperm(m);
    
    batch_x = train_x( :, kk(((i-1)*batchSize+1): i*batchSize) );
    batch_y = train_y( :, kk(((i-1)*batchSize+1): i*batchSize) );
    [cost, nn] = build_one_layer_addWeight(nn, batch_x ,batch_y);
    L = [L,cost];

end



end

function [ cost, nn ] = build_one_layer_addWeight( nn, x, y )

% initialize the parameter
lambda = nn.lambda;
LearnRate = nn.LearnRate;
W1 = nn.W1;
b1 = nn.b1;
W2 = nn.W2;
b2 = nn.b2;

W1grad = zeros(size(W1));
b1grad = zeros(size(b1));
W2grad = zeros(size(W2));
b2grad = zeros(size(b2));

%% BP algorithm
m = size(x,2);

% Denoising Autoencoder
x = x.*(rand(size(x)) > nn.DenoisingPara);

% feedforward
z2 = W1* x+ repmat(b1,1,m);
a2 = sigmoid(z2);
z3 = W2* a2+ repmat(b2,1,m);
a3 = sigmoid(z3);

cost = 0.5/m.* sum(sum((y - a3).^2))+ 0.5*lambda.* (sum(W1(:).^2)+sum(W2(:).^2));

% Back forword calculator the grad
d3 = -(y - a3).* a3 .*(1-a3);
d2 =  W2'* d3 .* a2 .*(1-a2);

W2grad = 1.0/m.* (d3 *a2')+ lambda.* W2;
b2grad = 1.0/m.* sum(d3,2);
W1grad = 1.0/m.* (d2 *x')+ lambda.*W1;
b1grad = 1.0/m.* sum(d2,2);


W2 = W2 - LearnRate*W2grad;
b2 = b2 - LearnRate*b2grad;
W1 = W1 - LearnRate*W1grad;
b1 = b1 - LearnRate*b1grad;

%grad = [ W1grad(:);b1grad(:);W2grad(:);b2grad(:) ];

nn.W1 = W1;
nn.b1 = b1;
nn.W2 = W2;
nn.b2 = b2;

end



function sigm = sigmoid(x)
    sigm = 1./(1+exp(-x));
end

function [ nn ] = theta_initialization( nn )

visibleSize = nn.visibleSize;
hiddenSize = nn.hiddenSize;

switch nn.Method
    case 'unsupervise'
        outputSize = nn.visibleSize;
    case 'supervise'
        outputSize = nn.outputSize;
    otherwise
        error('nn.Method error');
end  

r  = sqrt(6) / sqrt(hiddenSize+visibleSize+1);   % weights uniformly from the interval [-r, r]
W1 = rand(hiddenSize, visibleSize) * 2 * r - r;
r  = sqrt(6) / sqrt(hiddenSize+outputSize+1);
W2 = rand(outputSize, hiddenSize) * 2 * r - r;

b1 = zeros(hiddenSize, 1);
b2 = zeros(outputSize, 1);

nn.W1 = W1;
nn.b1 = b1;
nn.W2 = W2;
nn.b2 = b2;

end

function  label = predict( nn, x)
%UNTITLED3 Summary of this function goes here
%   Detailed explanation goes here

W1 = nn.W1;
b1 = nn.b1;
W2 = nn.W2;
b2 = nn.b2;

m = size(x,2);
label = zeros(1,m);


z2 = W1*x +repmat(b1,1,m);
a2 = sigmoid(z2);
z3 = W2*a2 +repmat(b2,1,m);
a3 = sigmoid(z3);

[~,label] = max(a3,[],1);


end


function sigm = sigmoid(x)
    sigm = 1./(1+exp(-x));
end

function r=visualize(X, mm, s1, s2)
%FROM RBMLIB http://code.google.com/p/matrbm/
%Visualize weights X. If the function is called as a void method,
%it does the plotting. But if the function is assigned to a variable 
%outside of this code, the formed image is returned instead.
if ~exist('mm','var')
    mm = [min(X(:)) max(X(:))];
end
if ~exist('s1','var')
    s1 = 0;
end
if ~exist('s2','var')
    s2 = 0;
end
    
[D,N]= size(X);
s=sqrt(D);
if s==floor(s) || (s1 ~=0 && s2 ~=0)
    if (s1 ==0 || s2 ==0)
        s1 = s; s2 = s;
    end
    %its a square, so data is probably an image
    num=ceil(sqrt(N));
    a=mm(2)*ones(num*s2+num-1,num*s1+num-1);
    x=0;
    y=0;
    for i=1:N
        im = reshape(X(:,i),s1,s2)';
        a(x*s2+1+x : x*s2+s2+x, y*s1+1+y : y*s1+s1+y)=im;
        x=x+1;
        if(x>=num)
            x=0;
            y=y+1;
        end
    end
    d=true;
else
    %there is not much we can do
    a=X;
end

%return the image, or plot the image
if nargout==1
    r=a;
else

    imagesc(a, [mm(1) mm(2)]);
    axis equal
    colormap gray

end