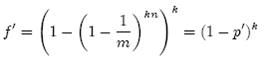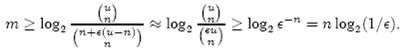Bloom Filter概念和原理

Bloom Filter概念和原理

原文地址：http://blog.csdn.net/jiaomeng/archive/2007/01/27/1495500.aspx

 

Bloom Filter 是一种空间效率很高的随机数据结构，它利用位数组很简洁地表示一个集合，并能判断一个元素是否属于 这个集合。 Bloom Filter 的这种高效是有一定代价的：在判断一个元素是否属于某个集合时，有可能会把不属于这个集合的元素误 认为属于这个集合（ false positive ）。因此， Bloom Filter 不适合那些“零错误”的应用场合。而在能容忍低错误率的应用场合下， Bloom Filter 通过极少的错误换取了存储空间的极大节省。

集 合表示和元素查询

下面我们具体来看 Bloom Filter 是如何用位数组表示集合的。初始状态时， Bloom Filter 是一个包含 m 位的位 数组，每一位都置为 0 。

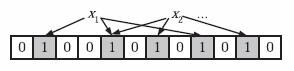
为了表达 S={x₁ , x₂ ,…,x_n } 这样一个 n 个元素 的集合， Bloom Filter 使用 k 个相互独立的哈希函数（ Hash Function ），它们分别将集合中的每个元素映射到 {1,…,m} 的范围中。对任意一个元素 x ，第 i 个哈希函数映射的位置 h_i (x) 就会被置为 1 （ 1 ≤ i ≤ k ）。注意，如果一个位置多次被置为 1 ，那 么只有第一次会起作用，后面几次将没有任何效果。在下图中， k=3 ，且有两个哈希函数选中同一 个位置（从左边数第五位）。    

 

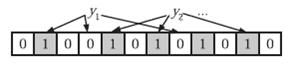
在判断 y 是否 属于这个集合时，我们对 y 应用 k 次哈希函数，如果所有 h_i (y) 的位置都是 1 （ 1 ≤ i ≤ k ），那么我们就认为 y 是集合 中的元素，否则就认为 y 不是集合中的元素。下图中 y₁ 就不是集合中的元素。 y₂ 或者属于这个集合，或者刚好是一个 false positive 。

错 误率估计

前面我们已经提到了， Bloom Filter 在判断一个元素是否属于它表示的集合时会有一定的错误率（ false positive rate ），下面我们就来估计错误率的大小。在估计之前为了简化模型，我们假设 kn<m 且各个哈希函数是完全随机的。当集合 S={x₁ , x₂ ,…,x_n } 的所有元素都被 k 个哈希 函数映射到 m 位的位数组中时，这个位数组中某一位还是 0 的概 率是：

其中 1/m 表示任意一个哈希函数选中这 一位的概率（前提是哈希函数是完全随机的）， (1-1/m) 表示哈希一次没有选中这一位 的概率。要把 S 完全映射到位数组中，需要做 kn 次哈 希。某一位还是 0 意味着 kn 次哈希都没有选中它，因此这 个概率就是（ 1-1/m ）的 kn 次方。令 p = e^-kn/m 是为了简化运算，这里用到了计算e时常用的近似：

 

令 ρ为 位数组中 0 的比例，则 ρ的数学 期望E( ρ)= p’ 。在 ρ已知的情况 下，要求的错误率（ false positive rate ）为：

(1- ρ) 为 位数组中 1 的比例， (1- ρ)^k 就表示 k 次哈希都刚好选中 1 的区域，即 false positive rate 。上式中第二步近似在前面已经提到了，现在来看第一步近似。 p’ 只是 ρ的数学期望， 在实际中ρ的值有可能偏离它的数学期望值。 M. Mitzenmacher 已经证明 ^[2] ，位数组中0 的比例非常集中地分布在它的数学期望值的附近。因此， 第一步的近似得以成立。分别将 p 和 p’ 代入上式中，得：

   

   

相比 p’ 和 f’ ，使用 p 和 f 通常在分析中更为方便。

最 优的哈希函数个数

既然 Bloom Filter 要靠多个哈希函数将集合映射到位数组中，那么应该选择几个哈希函数才能使元素查询时的错误率降到最低 呢？这里有两个互斥的理由：如果哈希函数的个数多，那么在对一个不属于集合的元素进行查询时得到 0 的概 率就大；但另一方面，如果哈希函数的个数少，那么位数组中的 0 就多。为了得到最优的哈希函数个 数，我们需要根据上一小节中的错误率公式进行计算。

 

先用 p 和 f 进行计算。注意到 f = exp(k ln(1 − e^−kn/m )) ，我们令 g = k ln(1 − e^−kn/m ) ，只要让 g 取到最 小， f 自然也取到最小。由于 p = e^-kn/m ，我们可以将 g 写成

根据对称性法则可以很容易看出当 p = 1/2 ，也就是 k = ln2· (m/n) 时， g 取得最小值。在这种情况下，最小错误率 f 等于 (1/2)^k ≈ (0.6185)^m/n 。另外，注意到p是位数组中某一位仍是0的概率，所以p = 1/2 对应着位数组中0和1各一半。换句话说，要想保持错误率低，最好让位数组有一半还空着。

 

需要强调的一点是， p = 1/2 时错误率最小这个结果并不依赖于近似值 p 和 f 。同样对于 f’ = exp(k ln(1 − (1 − 1/m)^kn )) ， g’ = k ln(1 − (1 − 1/m)^kn ) ， p’ = (1 − 1/m)^kn ，我们可以将 g’ 写成

同样根据对称性法则可以得到当 p’ = 1/2 时， g’ 取得最小值。

位 数组的大小

下面我们来看看，在不超过一定错误率的情况下， Bloom Filter 至少需要多少位才能表示全集中任意 n 个元 素的集合。假设全集中共有 u 个元素，允许的最大错误率为 є ，下面 我们来求位数组的位数 m 。

 

假设 X 为全 集中任取 n 个元素的集合， F(X) 是 表示 X 的位数组。那么对于集合 X 中任意 一个元素 x ，在 s = F(X) 中查询 x 都能得到肯定的结果，即 s 能够接 受 x 。显然，由于 Bloom Filter 引入了错误， s 能够接 受的不仅仅是 X 中的元素，它还能够 є (u - n) 个 false positive 。因此，对于一个确定的位数组来说，它能 够接受总共 n + є (u - n) 个元素。在 n + є (u - n) 个元素中， s 真正表 示的只有其中 n 个，所以一个确定的位数组可以表示

个集合。 m 位的位数组共有 2^m 个不同的组合，进而可以推出， m 位的位 数组可以表示

   

个集合。全集中 n 个元素 的集合总共有

   

个，因此要让 m 位的位 数组能够表示所有 n 个元素的集合，必须有

   

即：

   

上式中的近似前提是 n 和 єu 相比很小，这也是实际情况中常常发生的。根据上式，我们得出结论：在错误率不大于 є 的情况下， m 至少要 等于 n log₂ (1/є) 才能表示任意 n 个元素 的集合。

 

上一小节中我们曾算出当 k = ln2· (m/n) 时错误率 f 最小， 这时 f = (1/2)^k = (1/2)^{mln2 / n} 。现在令 f ≤ є ，可以推出

这个结果比前面我们算得的下界 n log₂ (1/є) 大了 log₂ e ≈ 1.44 倍。这说明在哈希函数的个数取到最优时，要让错误率不超过 є ， m 至少需要取到最小值的 1.44 倍。

总 结

在计算机科学中，我们常常会碰到时间换空间或者空间换时间的情况， 即为了达到某一个方面的最优而牺牲另一个方面。 Bloom Filter 在时间空间这两个 因素之外又引入了另一个因素：错误率。在使用 Bloom Filter 判断一个元素是否 属于某个集合时，会有一定的错误率。也就是说，有可能把不属于这个集合的元素误认为属于这个集合（ False Positive ），但不会把属于这个集合的元素误认为不属于这个集合（ False Negative ）。在增加了错误率这个因素之后， Bloom Filter 通过允许少量的错误来节省大量的存储空间。

 

自从 Burton Bloom 在 70 年代提出 Bloom Filter 之后， Bloom Filter 就被广 泛用于拼写检查和数据库系统中。近一二十年，伴随着网络的普及和发展， Bloom Filter 在网络领域获得了新生，各种 Bloom Filter 变种和新的应用不断出现。可以预见，随着网络应用的不断深入，新的变种和应用将会继续出现， Bloom Filter 必将获得更大的发展。

参 考资料

[1] A. Broder and M. Mitzenmacher. Network applications of bloom filters: A survey . Internet Mathematics, 1(4):485–509, 2005.

[2] M. Mitzenmacher. Compressed Bloom Filters . IEEE/ACM Transactions on Networking 10:5 (2002), 604—612.

[3] www.cs.jhu.edu/~fabian/courses/CS600.624/slides/bloomslides.pdf

[4] http://166.111.248.20/seminar/2006_11_23/hash_2_yaxuan.ppt