哈夫曼树的构造
构造哈夫曼树的过程是这样的
一、构成初始集合
对给定的n个权值{W1,W2,W3,...,Wi,...,Wn}构成n棵二叉树的初始集合F={T1,T2,T3,...,Ti,...,Tn}，其中每棵二叉树Ti中只有一个权值为Wi的根结点，它的左右子树均为空。（为方便在计算机上实现算法，一般还要求以Ti的权值Wi的升序排列。）
二、选取左右子树
在F中选取两棵根结点权值最小的树作为新构造的二叉树的左右子树，新二叉树的根结点的权值为其左右子树的根结点的权值之和。
三、删除左右子树
从F中删除这两棵树，并把这棵新的二叉树同样以升序排列加入到集合F中。
四、重复二和三两步，
重复二和三两步，直到集合F中只有一棵二叉树为止。
举个例子
有个序列是(7,9,2,6,32,3,21,10)
叫你求哈夫曼树
步骤一：把这些点都看成是一个只有根结点的树的集合F
步骤二，选2个值最小的树
步骤三：在这些树的集合F中删除这2棵树
然后把 
构成一颗二叉树
变成了
（5 = 2 + 3）
然后把这个树加入到集合F
5代表这棵树的权值
然后继续上述步骤
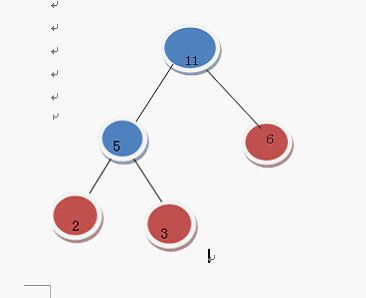
肯定是选 5 和 6
把这2个构成二叉树
在F中删除5 6 加入11这棵树
变成了
继续上述步骤
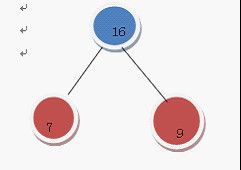
选7 和 9
在F中删除7 和9
加入16这棵树
变成了
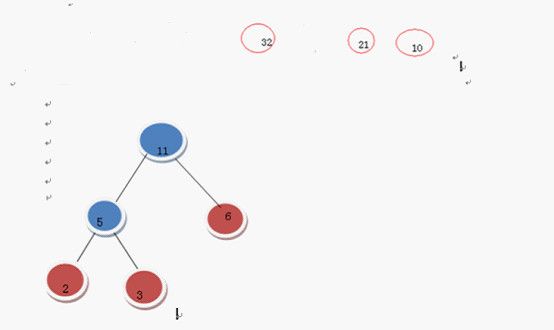
继续上述步骤
选 10 和11
在F中删除10 和11 加入21这棵树
继续上述步骤
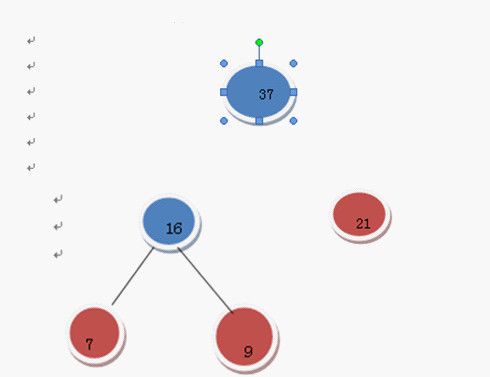
选16和21 （有2个21，随便选哪个）
我选那个只有一个根结点的21好了
16和21构成二叉树
在F中删除这16和21这两棵树
加入37这棵树
继续上述步骤
选21和32
构成二叉树
在F中删除21和32这2两棵树
加入53这棵树
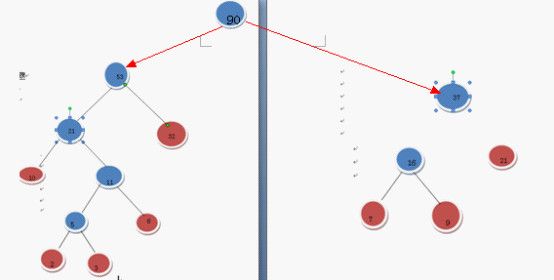
还是继续上面步骤
把F中的两棵树合并成一棵树
