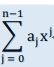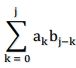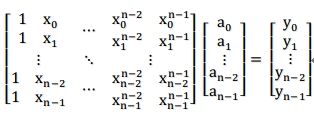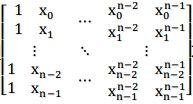快速傅立叶变换_FFT
快速傅立叶变换FFT
下面的排版比较乱，可以直接下word版的：http://minus.com/dbdrNFtIEL89Eb.docx；
原理：利用多项式点值求积的便捷性。
对于一个次数界为n的多项式A(x) = 
然后我们对于这种多项式有很多表示方法，最常见的就是系数表示法(coefficient representation)，也就是我们定义一个向量a = (a0, a1, a2,…, an-1),通过向量a，我们就知道了这个多项式的所有系数，这样对于多项式与多项式就能进行运算了：
1.多项式加法：A(x) + B(x) = C(x)
显然，C(x)的系数向量c = (a0 + b0, a1 + b1, ……, an – 1 + bn – 1)
时间复杂度：O(n)
2.多项式乘法：A(x) * B(x) = C(x)
看上去乘法要比加法复杂得多：
对于向量c 中的第j项cj =
这个自己画几个式子推一下就很好理解，但它的时间复杂度是O(n^2)的
下面我们再来看看另一种对于多项式的表示方法：点值表示法(point-value representation)
对于A(n)我们使用n个点值对所形成的集合来表示：
{(x0, y0), (x1, y1), ……, (xn – 1, yn – 1)}
对于这个点值对，就相当于以多项式的元为自变量，以多项式的值为值的一个函数在坐标系上经过的点的坐标，即：
yk = A(xk)
这就好像已知了一个1元n次方程组，我们能够求出函数式一样，我们可以使用这样的形式来表示一个多项式。
那么，我们如果已知了一个多项式的系数表示，怎样能得到它的点值表示呢？
很显然一个多项式的点值表示，不是唯一的，我们可以选取n个不同的x值，将它们代入多项式中求出对应的y，即:
这样就能得到多项式的一种点值表示，现在，如果我们已知了点值表示，又怎样求出多项表示呢？
我们设形如
为V(x0, x1, x2, ……, xn – 1)， 这其实就是一个范德蒙德矩阵，它的行列式的值为：
显然这个值不是零，那么这个矩阵非奇异，也就有其自己的逆，
那么我们就可以通过点值表示求出其系数表示，即：
a = V（x0, x1, x2, ……, xn – 1）-1 * y
现在我们再来看看点值表示下的多项式运算：
1.加法： A(x) + B(x) = C(x)
那么c的点值表示为：{(x0, ya0 + yb1), (x1, ya2 + yb2), ……, (xn – 1, yan – 1 + ybn – 1)}
这就相当于两个方程组的叠加。
2.乘法：A(x) * B(x) = C(x)
C 的点值表示为：{(x0, ya0 * yb1), (x1, ya2 * yb2), ……, (xn – 1, yan – 1 * ybn – 1)}
点值表示在这里显示出了其强大的优势，因为这个运算是O(n)的!
那么回到正题，我们的FFT就是对于两个多项式利用点值表示的性质来加快乘法运算的速度！
不过大家都知道我们通常所说的FFT都是O(nlogn)的，这个复杂度是耗在哪里了呢？ 就是在刚才没有详细分析的系数表示与点值表示的互相转换里面了。
我们再来看系数表示向点值表示的转换：V矩阵与a矩阵的互乘求出了y矩阵，这暴力来算是O(n^2)的，相对应的，点值表示向系数表示转换通过基于拉格朗日算法的优化之后也是O(n^2)的，我们仍然需要更高效的算法。
现在的瓶颈就在于两个转换了，要解决这个问题，我们要了解几个玩意儿：
1. 单位负根
N次单位负根是值满足
的复数
， 我们可以想象成将一个复数平面按角度平均分成了n份，恰好有n个根
，
，那么显然：
值
称为这个单位负根的主根，其他的根则是以n为周期的它的幂。
单位负根有一些非常美妙的定理和推论，等一下要用的时候再证。
2. 离散傅立叶变换(Discrete Fourier Transform, DFT)
设我们现在希望快速转换的多项式为：
A(x) =
我们现在已知了它的系数表示，需要快速求出一个点值表示.
那么单位负根出现了，前面讲到了，点值表示中的那些自变量x是可以由我们决定的，那么我们现在就把
,
,拿来作为这n个自变量，结果y矩阵的值就可以这样来求：
yk= A(
) = 
这样求出来的y集就被称为原多项式的离散傅立叶变换，即
y = DFTn(a)
3. 快速傅立叶变换(Fast Fourier Transform, FFT)
可以看出，使用原DFT的定义来求y的时间复杂度是O(n)的，FFT利用了单位负根的性质，将复杂度降到了O(nlogn)。
对于一个我们将变换的次数界为n的多项式，我们现在已知它的系数多项式：
A(x) = a0 + a1x + a2x2 + a3x3 + …… + an-1xn-1
那么我们定义两个新的次数界为n/2的多项式(暂且认为n为偶数)A[0](x)和A[1](x)，他们的系数分别为原多项式A(x)的偶数下标的系数和奇数下标的系数，即：
A[0](x) = a0 + a2x + a4x2 + …… an – 2xn/2-1
A[1](x) = a1 + a3x + a5x2 + …… an – 1xn/2-1
这样显然就有了：
A(x) = A[0](x2) + xA[1](x2)
我们再来看当以单位负根为x集时的形式：
A
= A[0]
+
A[1]
k
这个时候就要用到单位负根的性质了：
单位负根的相消引理：对于非负整数n,k和正整数d，有
简单证明：由单位负根的定义：
单位负根的折半引理：
这个直接由相消引理可得。
对于A[0]
+
A[1]
k
，本来我们是要求出A[0] 与 A[1] 中的n个
的次幂值：
，
，
，……， 
由于折半引理可得形如这些值都有与之对应的n/2次的单位负根的值与其相等，而显然n/2次的单位负根的值只有n/2种且以n/2为周期，因此我们本来要求n个值，现在却只需要求出n/2个值就能够确定所有的数的值了。
这里我们再使用单位负根的一个美妙的性质：
这个根据
可以直接出来
有了这个式子，我们就可以值求n/2个值得到所有负根次幂的值了。
这样我们就划出了子问题，即A
= A[0]
+
A[1]
k
,可以无限递归下去，这些子问题与原问题相同，但规模缩小一半，因此我们成功地将一个DFTn(x)转化成两个DFTn/2(x)问题， 这就是FFT的基础，为了计算方便，我们可以将n扩充成2的次幂的形式。
通过这样的递归处理，我们终于可以把复杂度降低到了O(nlogn)。
至此，我们把一个多项式的系数表示专成了其点值表示，然后我们可以利用点值表示的性质，直接在O(n)的时间内求出两个多项式乘积的点值表示，现在最后的问题就是怎样将其转回系数表示。
因为y=Vn a，因此我们要求出a，只需要求出Vn-1 y，Vn-1就是原矩阵的逆矩阵，得到了，现在我们证明一个结论：
对于Vn-1 中的(j, k)处的值为
.
因为Vn * Vn-1 = 单位矩阵，故只有在对角线上的数为1，其他地方都为零，所以我们设ai,j为正矩阵(I,j)上的值，bi,j为逆矩阵(I,j)上的值，ci,j为单位矩阵(I,j)上的值，则：
Ci,j= 
前面对于这个逆矩阵的结论，我还没有完全搞懂，因为仍然对于矩阵的初等变换不是十分熟悉，这个工作留待以后再做。
反正我们可以知道如果这样构造出一个矩阵，它与原来的正矩阵的乘积的值为1，所以暂且这样接受。
求出了逆矩阵，我们像正变换一样对答案的点值表示进行一次FFT，就能够得到系数表示了。
搞了几天，写了递归版的FFT，还有效率高一点的迭代版，不过考虑到这个的应用面并不太广，我把这个排到以后再去做，这里贴一下我的很丑的FFT：
#include <stdio.h>
#include <string.h>
#include <math.h>
#include <memory.h>
const int nmax = 50000, lmax = 1 << 15, mo = 10000, wmax = 4, pe[4] = {1, 10, 100,1000};
#define Pi M_PI
struct complex
{
double re, ur;
}A[lmax + 18], B[lmax + 18], wtmp, atmp[lmax + 18], ul[lmax + 18];
int l = 1, n;
char str[nmax + 18];
int ans[lmax + 18];
complex operator+(complex a, complex b)
{
a.re += b.re;
a.ur += b.ur;
return a;
}
complex operator-(complex a, complex b)
{
a.re -= b.re;
a.ur -= b.ur;
return a;
}
complex operator*(complex a, complex b)
{
complex c;
c.re = a.re * b.re - a.ur * b.ur;
c.ur = a.re * b.ur + a.ur * b.re;
return c;
}
void fft(complex *a, int n, int step)
{
if (n == 1)
return;
int bs = step << 1;
fft(a, n >> 1, bs);
fft(a + step, n >> 1, bs);
for (int i = 0, tmp = 0; tmp < (n >> 1); i += bs, ++tmp)
{
wtmp = ul[i >> 1] * a[i + step];
atmp[tmp] = a[i] + wtmp;
atmp[tmp + (n >> 1)] = a[i] - wtmp;
}
for (int i = 0, tmp = 0; tmp < n; i += step, ++tmp)
a[i] = atmp[tmp];
}
bool get(complex *a)
{
if (scanf("%s\n", str + 1) == EOF) return false;
int len = strlen(str + 1), wei = 0, tmp = 0, bi = -1;
for (int i = len; i; --i)
{
tmp = tmp + (str[i] - '0') * pe[wei++];
if (wei == wmax)
a[++bi].re = tmp, tmp = wei = 0;
}
if (tmp) a[++bi].re = tmp;
if (bi > n) n = bi;
return true;
}
int main()
{
get(A);
get(B);
while (l < n) l <<= 1;
l <<= 1;
for (int i = 0; i < l; ++i)
{
ul[i].re = cos(2 * Pi * i / l);
ul[i].ur = sin(2 * Pi * i / l);
}
fft(A, l, 1);
fft(B, l, 1);
for (int i = 0; i < l; ++i)
A[i] = A[i] * B[i], ul[i].ur = -ul[i].ur;
fft(A, l, 1);
long long x = 0;
for (int i = 0; i < l; ++i)
{
x += (long long) (A[i].re / l + 0.1);
ans[i] = x % mo;
x /= mo;
}
while (l && !ans[l]) --l;
printf("%d", ans[l--]);
for (int i = l; i >= 0; --i)
printf("%04d", ans[i]);
return 0;
}