傅里叶变换的意义 .
傅里叶变换就是将满足一定条件的某个函数表示成三角函数(正弦/余弦)或其积分的线性组合。傅里叶变换可以看出一种工具,将一个连续的信号(不方便处理)转换成一个个小信号的叠加(好处理)。就是将信号完成从时域表示到频域表示。信号本质没有变,转换后有助于后续处理。来看一个图,原图1-4及代码转自http://fashionxu.bokee.com/4632908.html ,第5个图是我加的。
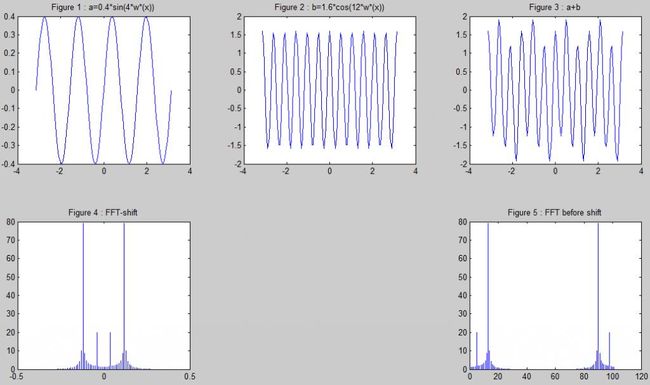
图3是由图1和图2两个三角函数波合成的,但是在时域表示下,很难对图3进行分析,于是,对图3执行傅里叶变换,转换到频域表示,如图5,就很明显。又但是,因为MATLAB FFT函数直接转换出来的数据与频率坐标是不对应的,所以用ffshift函数将零频点移到频谱中间,如图4,这样方便观看。图5的横坐标表示频率,纵坐标表示幅值。不看负频部分,从正频部分来看,里0点近的表示频率小,幅值小,对应图1中的a;离0点远的表示频率大,幅值大,对应图2中的b(请自动忽略图5的横坐标)。
PS:在信号在时域无限(一直连续)的情况下,图5应该是2高2低的4条谱线;但由于时域是有限的,所以存在一些其他频率的点。
再PS:关于如何理解负频,这里有个帖子有很多讨论:http://bbs.cnttr.com/archiver/tid-73802.html
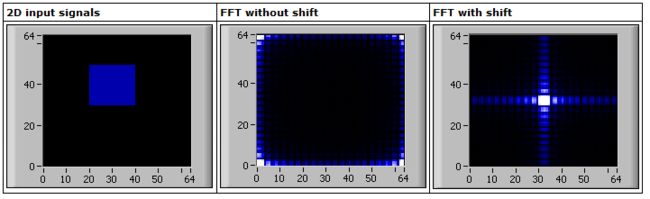
shift的作用,在2维傅里叶变换上看更有效果。左图是原图像,中图是傅里叶变换之后的图像,但是低频部分在图像边缘,不明显,shift以后,低频部分被移到了中心。图像来自http://zone.ni.com/reference/en-XX/help/371361F-01/lvanls/fft/
下面的转述来自网络,也说明了傅里叶变换的物理意义:
傅里叶变换就是将一个信号的时域表示形式映射到一个频域表示形式;逆傅里叶变换恰好相反。这都是一个信号的不同表示形式。它的公式会用就可以,当然把证明看懂了更好。
对一个信号做傅立叶变换,可以得到其频域特性,包括幅度和相位两个方面。幅度是表示这个频率分量的大小,那么相位呢,它有什么物理意义?频域的相位与时域的相位有关系吗?信号前一段的相位(频域)与后一段的相位的变化是否与信号的频率成正比关系。
傅立叶变换就是把一个信号,分解成无数的正弦波(或者余弦波)信号。也就是说,用无数的正弦波,可以合成任何你所需要的信号。
想一想这个问题:给你很多正弦信号,你怎样才能合成你需要的信号呢?答案是要两个条件,一个是每个正弦波的幅度,另一个就是每个正弦波之间的相位差。所以现在应该明白了吧,频域上的相位,就是每个正弦波之间的相位。
傅立叶变换用于信号的频率域分析,一般我们把电信号描述成时间域的数学模型,而数字信号处理对信号的频率特性更感兴趣,而通过傅立叶变换很容易得到信号的频率域特性
傅里叶变换简单通俗理解就是把看似杂乱无章的信号考虑成由一定振幅、相位、频率的基本正弦(余弦)信号组合而成,傅里叶变换的目的就是找出这些基本正弦(余弦)信号中振幅较大(能量较高)信号对应的频率,从而找出杂乱无章的信号中的主要振动频率特点。如减速机故障时,通过傅里叶变换做频谱分析,根据各级齿轮转速、齿数与杂音频谱中振幅大的对比,可以快速判断哪级齿轮损伤。
第一个图的MATLAB代码如下:
w=2*pi;
x = -0.5:0.01:0.5;
a=0.4*sin(4*w*(x));
b=1.6*cos(12*w*(x));
subplot(2,3,1);
plot(w*x,a),title('Figure 1 : a=0.4*sin(4*w*(x))');
subplot(2,3,2);
plot(w*x,b),title('Figure 2 : b=1.6*cos(12*w*(x))');
subplot(2,3,3);
plot(w*x,a+b),title('Figure 3 : a+b');
c=fft(a+b);
subplot(2,3,4);
stem(x,fftshift(abs(c)),'Marker','none'),title('Figure 4 : FFT-shift');
subplot(2,3,6);
stem(abs(c),'Marker','none'),title('Figure 5 : FFT before shift');