最小生成树Kruskal算法(邻接矩阵和邻接表)
最小生成树,克鲁斯卡尔算法.
算法简述:
将每个顶点看成一个图.
在所有图中找权值最小的边.将这条边的两个图连成一个图,
重复上一步.直到只剩一个图.
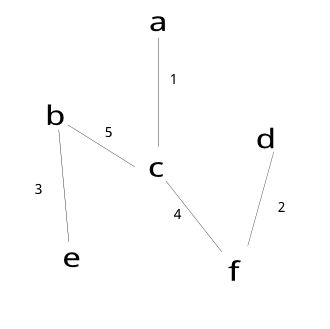
注:将abcdef每个顶点看成一个图.将最小权值的边的两个图连接.
连接最小权值为1的两个图,这时a-c,b,d,e,f.
连接最小权值为2的两个图,这时a-c,b,d-f,e.
连接最小权值为3的两个图,这时a-c,b-e,d-f.
连接最小权值为4的两个图,这时a-c-f-d,b-e.(c-f)
连接最小权值为5的两个图,这时a-c-b-e-f-d.(b-c)
结束.
根据上述操作,我们需要一个存储边信息的数组(Edge结构体),Edge包含了边的两个节点和权值.
1 typedef struct 2 { 3 int head;//边的始点下标 4 int tail;//边的终点下标 5 int power;//边的权值 6 } Edge;
还需要一个visited数组,用来标识图中的节点信息.
算法操作:
初始化一棵树(用来保存最小生成树,直接输出也行.)
将图中所有边复制到一个数组中,将数组排序(递增顺序)
将小边的两个顶点连接.将两个图合并成一个图.
重复上一步.
临街矩阵的代码实现
代码中,ijk做循环用,v1,v2做边的两个顶点信息的下标,vs1,vs2做标识v1和v2所属图
1-27行,初始化visited,edge,kruskal_tree等信息.
29-44行,生成一棵最小生成树.
35行,if是为了防止回路,vs1和vs2标识一个这两点是否属于一个图.
38行,for是为了将visited数组中vs2边成vs1,因为这时,v1和v2已经在一个图里了.
1 void kruskal(Graph * graph, Graph * kruskal_tree) 2 { 3 int visited[graph->vertexs]; 4 Edge edge[graph->brim]; 5 int i, j, k; 6 int v1, v2, vs1, vs2; 7 8 for ( i = 0; i < graph->vertexs; i++ ) 9 visited[i] = i; 10 11 k = 0; 12 for ( i = 0; i < graph->vertexs; i++ ) 13 { 14 for ( j = i + 1; j < graph->vertexs; j++ ) 15 { 16 if ( graph->arcs[i][j] != MAX_VALUE ) 17 { 18 edge[k].head = i; 19 edge[k].tail = j; 20 edge[k].power = graph->arcs[i][j]; 21 k++; 22 } 23 } 24 } 25 26 init_kruskal(graph, kruskal_tree); 27 my_sort(edge, graph->brim); 28 29 for ( i = 0; i < graph->brim; i++ ) 30 { 31 v1 = edge[i].head; 32 v2 = edge[i].tail; 33 vs1 = visited[v1]; 34 vs2 = visited[v2]; 35 if ( vs1 != vs2 ) 36 { 37 kruskal_tree->arcs[v1][v2] = graph->arcs[v1][v2]; 38 for ( j = 0; j < graph->vertexs; j++ ) 39 { 40 if ( visited[j] == vs2 ) 41 visited[j] = vs1; 42 } 43 } 44 } 45 }
临街矩阵源码:http://www.cnblogs.com/ITgaozy/p/5200637.html
邻接表的代码实现
17行,if是为了将防止边的重复输入(在邻接矩阵中,点在矩阵中是对称的,所以我们只输入一个上三角中的数据就够了.但在邻接表中,我们如何判断一条边是否已经输入过了? 我的方法是将比当前节点下标大的输入,例如右a,b两个节点,a的节点小与b,我们在输入b的信息时,由于a的节点下标比b小,不输入a-b这条边,因为我们在输入a的信息时,a-b这条边已经输入过了.
1 void kruskal(Graph * graph, Graph * kruskal_tree) 2 { 3 int visited[graph->vertexs]; 4 int i, j; 5 Edge edge[graph->brim]; 6 int v1, v2, vs1, vs2; 7 Arc_node * cur, * tmp; 8 9 for ( i = 0; i < graph->vertexs; i++ ) 10 visited[i] = i; 11 12 for ( i = 0, j = 0; i < graph->vertexs; i++ ) 13 { 14 cur = graph->adjlist[i].next; 15 while ( cur != NULL ) 16 { 17 if ( cur->pos > i ) 18 { 19 edge[j].head = i; 20 edge[j].tail = cur->pos; 21 edge[j].power = cur->distance; 22 j++; 23 } 24 cur = cur->next; 25 } 26 } 27 28 init_kruskal(graph, kruskal_tree); 29 my_sort(edge, graph->brim); 30 31 for ( i = 0; i < graph->brim; i += 1 ) 32 { 33 v1 = edge[i].head; 34 v2 = edge[i].tail; 35 vs1 = visited[v1]; 36 vs2 = visited[v2]; 37 if ( vs1 != vs2 ) 38 { 39 if ( kruskal_tree->adjlist[v1].next == NULL ) 40 { 41 kruskal_tree->adjlist[v1].next = make_node(v2, edge[i].power); 42 } 43 else 44 { 45 tmp = kruskal_tree->adjlist[v1].next; 46 while ( tmp->next != NULL ) 47 tmp = tmp->next; 48 tmp->next = make_node(v2, edge[i].power); 49 } 50 for ( j = 0; j < graph->vertexs; j++ ) 51 { 52 if ( visited[j] == vs2 ) 53 visited[j] = vs1; 54 } 55 } 56 } 57 }
邻接表源码:http://www.cnblogs.com/ITgaozy/p/5200643.html