Binary Search Tree/ Binary Sorted Tree —— BST

Binary tree

2015.03.17更新

注意, 二叉查找树又称作二叉排序树(子节点与父亲节点的数值关系是确定的).

                     In computer science, a binary tree is a tree data structure in which each node has at most two children (referred to as the left child and the right child). In a binary tree, the degree of each node can be at most two. Binary trees are used to implement binary search trees and binary heaps, and are used for efficientsearching and sorting. A binary tree is a special case of a K-ary tree, where k is 2.

这里要感谢@凯旋冲锋 ，他找到了一个很好的算法可视化网站。

http://visualgo.net/bst.html

Python实现：

"""
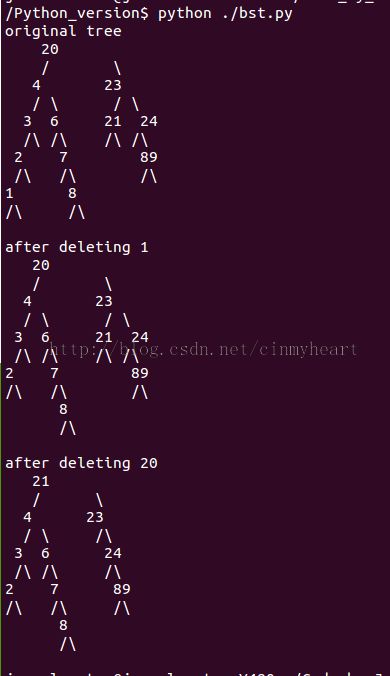
Code writer : EOF
Code date   : 2015.01.16
Code file   : bst.py
e-mail      : [email protected]

Code description:
        Here is a implementation for Binary search tree(BST)
which is coded by Python.

ATTENTION: Binary search tree do not allow the inputed data 
which have the same value! Make sure that every data you insert
into the tree is just only one but no more than two times.

        If there is something wrong with my code, please touch
me by e-mail. Thank you!
"""

class BST() :

    def __init__(self) :
        self.root   = None


    def insert(self, num) :
        if self.root == None :
            self.root = new_node(num)
        else :
            tmp_node = self.root
            par_node = None

            #Just for searching the location where could be inserted
            while tmp_node != None :
                if tmp_node.number > num :
                    par_node = tmp_node
                    tmp_node = tmp_node.left
                else :
                    par_node = tmp_node
                    tmp_node = tmp_node.right

            # After while loop, we found that location which's parent
            # is @par_node
            if par_node.number > num :
                par_node.left  = new_node(num)
                par_node.left.parent = par_node
                par_node.left.right  = None
                par_node.left.left   = None
                return par_node.left
            else :
                par_node.right = new_node(num)
                par_node.right.parent = par_node
                par_node.right.right  = None
                par_node.right.left   = None
                return par_node.right


    def search(self, node, num) :
        if node.number == num  or node == None:
            return node
        elif node.number > num :
            return self.search(node.left, num)
        elif node.number < num :
            return self.search(node.right, num)


    def delete(self, num) :
        z = self.search(self.root, num)
        if z.left == None or z.right == None :
            y = z
        else :
            y = self.tree_successor(z)

        if y.left != None :
            x = y.left
        else :
            x = y.right

        if x != None :
            x.parent = y.parent
        if y.parent == None :
            self.root = x
        elif y == y.parent.left :
            y.parent.left = x
        else :
            y.parent.right = x

        if y != z :
            # copy y's satelllite data into z
            z.number = y.number

    def tree_mininum(self, x) :
        while x.left != None :
            x = x.left
        return x


    def tree_maxinum(self, x) :
        while x.right != None :
            x = x.right
        return x

    def tree_successor(self, x) :
        if x.right != None :
            return self.tree_mininum(x.right)
         
        y = x.parent
        while y != None and x == y.right :
            x = y
            y = y.parent
        return y    

    def tree_predecessor(self, x) :
        if x.left != None :
            return self.tree_maxinum(x.left)

        y = x.parent
        while y != None and x == y.left :
            x = y.left
            y = y.parent

    def show(self, node) :
      if node == None :
          return None
      self.show(node.left)
      print " node ",node.number,

      if node.right != None :
         print " right child ", node.right.number,
      else :
         print "None",
      if node.left != None :
         print " left child ", node.left.number
      else :
         print "None"
      self.show(node.right)

    def __str__(self):
        def recurse(node) :
            if node is None:
                return [], 0, 0
            else :
                left_lines, left_pos, left_width = recurse(node.left)
                right_lines, right_pos, right_width = recurse(node.right)

                label = str(node.number)
                middle = max(right_pos + left_width - left_pos +1,
                        len(label), 2)

                pos    = left_pos + middle//2
                width  = left_pos + middle + right_width - right_pos

                while len(left_lines) < len(right_lines) :
                    left_lines.append(' ' * left_width)
                while len(right_lines) < len(left_lines) :
                    right_lines.append(' ' * right_width)

                line   = [' ' * left_pos + label + 
                          ' ' * (right_width-right_pos + 1),
                          ' ' * left_pos + '/' + 
                          ' ' * (middle-2) + '\\' +
                          ' ' * (right_width - right_pos)
                                    ] + \
                         [
                            left_line + 
                            ' ' * (width - left_width - right_width) +
                            right_line 
                            for left_line, right_line 
                            in zip(left_lines, right_lines)
                                    ]

                if node is self.root :
                    return line
                else :
                    return line, pos, width

        if self.root is None :
           return '<Empty tree>'

        output = recurse(self.root)
        for i in range(1, len(output)-2) :
          output[0] += '\n' + output[i]

        return output[0]+'\n'

class new_node() :

      def __init__(self, num = -1) :
          self.number = num
          self.right  = None
          self.left   = None
          self.parent = None

#--------------testing code----------------
A = [20,4,6,3,2,1,7,8,9,23,24,21,89,34]
my_bst = BST()

for i in range(0,len(A)-1) :
    my_bst.insert(A[i])

print "original tree"
print my_bst

my_bst.delete(1)

print "after deleting 1"
print my_bst

my_bst.delete(20)

print "after deleting 20"
print my_bst

下面的树形结果是测试结果，如果想知道如何打印的这种树形结构需要了解上述实现中的recurse()函数，对于recurse()函数的解析在这里

http://blog.csdn.net/cinmyheart/article/details/43151005

证明：如果二叉树中的某个节点有两个子女，则其后继没有左子女，其前驱没有右子女。

C语言实现：

bst.h

/*******************************************************************************
* code writer: EOF
* Date : 2014.02.20
* Update: 2015.01.26
* code purpose:
		This code is  for header file -- bst.h(Binary_Search_Tree)
*e-mail:[email protected]

If there somthing wrong with my code, please touch me by e-mail.Thank you!
*****************************************************************************/
#ifndef _BST_H
#define _BST_H 


#include<stdio.h>
#include<stdlib.h>

//definition for node structure
struct node
{
	int data;
	struct node* leftchild;	
	struct node* rightchild;
	struct node* parent;
};

//declaration for delete_note function
int delete_node(struct node* p_node,int number);

//declaration for insert_note function
struct node *insert_node(struct node* p_node,
                         struct node *p_parent,
                         int number);

//declaration for print_node function
int print_node(struct node* p_node);

//declaration for free_tree function
void free_tree(struct node* p_node);

//declaration for insert_for_delete function
int insert_for_delete(struct node* p_node,struct node* tmp);

#endif

binary_search_tree.c

/*******************************************************************************
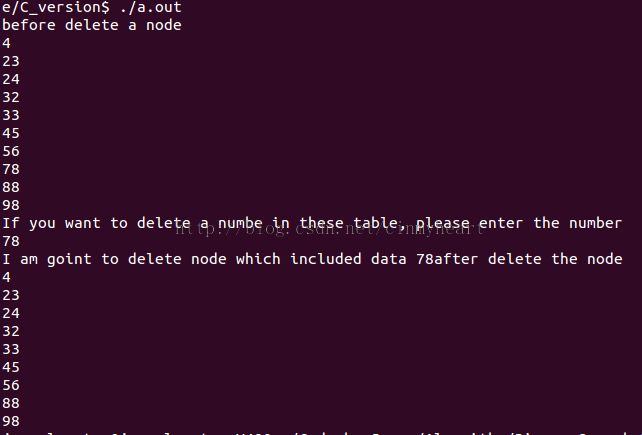
* code writer: EOF
* Date : 2014.02.20
* Update : 2015.01.26
* code purpose:
		This code is main function.
*e-mail:[email protected]

If there somthing wrong with my code, please touch me by e-mail.Thank you!
*****************************************************************************/
#include "stdio.h"
#include "stdlib.h"
#include "bst.h"

#define ARRAYSIZE 10


int main(int argc, char* argv[])
{
	int temp = 0;
	int number = 0;
	int array[ARRAYSIZE] = {23,32,4,56,33,98,24,88,45,78};
	
        struct node* root = NULL;

	for(temp = 0;temp < ARRAYSIZE;temp++)
	{
		if((root = insert_node(root, NULL, array[temp])) ==  NULL)
		{
			break;
                        //memory allocation failed ,
                        //so break out of this loop
		}
	}
	
	printf("before delete a node\n");
	print_node(root);

	printf("If you want to delete a numbe in these table,"
                " please enter the number\n");

	while(!scanf("%d",&number))
	{
                while(getchar() != '\n')
                {
   		    printf("scanf error!\nPlease enter again\n");
                }
	}

	printf("I am goint to delete node which included data %d",number);
	delete_node(root,number);
	
	printf("after delete the node\n");
	print_node(root);
	
	free_tree(root);
	return 0;
}

insert_node.c

/*********************************************************************
* Code writer:EOF
* Code date: 2014.02.20
* code purpose:
		this code is my implementation for the function insert_for_delete
* e-mail: [email protected]

If something wrong with my code, please touch me by e-mail. Thank you!

*********************************************************************/
#include "stdio.h"
#include "bst.h"

int insert_for_delete(struct node* p_node,struct node* tmp)
{
	if((p_node) == NULL)
	{
		return 0;
	}
	else
	{
		if((p_node)->data < tmp->data)
		{
			if(0 == insert_for_delete((p_node)->rightchild,tmp))
			{
				(p_node)->rightchild = tmp;
				tmp->parent = (p_node);
			}
		}
		else if((p_node)->data > tmp->data)
		{
			if(0 ==insert_for_delete((p_node)->leftchild,tmp))
			{
				(p_node)->leftchild = tmp;
				tmp->parent = (p_node);
			}
		}
	}
}

delete_node.c

/*******************************************************************************
* code writer: EOF
* Date : 2014.02.20
* code purpose:
		This code is my implementation for function -- delete_node
*e-mail:[email protected]

If there somthing wrong with my code, please touch me by e-mail.Thank you!
*******************************************************************************/
#include "bst.h"

int delete_node(struct node* p_node,int number)
{
	struct node* temp = NULL;

	if(p_node->data == number)
	{
		//when both the rightchild and leftchild of the node which is to be deleted are NULL
		if((p_node)->leftchild == NULL && (p_node)->rightchild == NULL)
		{
			if((p_node)->parent->rightchild == (p_node))
			{
				(p_node)->parent->rightchild = NULL;
				free((p_node));
			}
			else if((p_node)->parent->leftchild == (p_node))
			{
				(p_node)->parent->leftchild = NULL;
				free((p_node));
			}
		}

		//when the leftchild is NULL but the rightchild isn't NULL
		if((p_node)->leftchild == NULL && (p_node)->rightchild != NULL)
		{
			if((p_node)->parent->rightchild == (p_node))
			{
				(p_node)->parent->rightchild = (p_node)->rightchild;
				(p_node)->rightchild->parent = (p_node)->parent;
				free((p_node));
			}
			else if((p_node)->parent->leftchild == (p_node))
			{
				(p_node)->parent->leftchild = (p_node)->rightchild;
				(p_node)->rightchild->parent = (p_node)->parent;
				free((p_node));
			}
		}
		
		//when the rightchild is NULL but the leftchild isn't NULL
		if((p_node)->rightchild == NULL && (p_node)->leftchild != NULL)
		{
			if((p_node)->parent->rightchild == (p_node))
			{
				(p_node)->parent->rightchild = (p_node)->leftchild;
				(p_node)->leftchild->parent = (p_node)->parent;
				free((p_node));
			}
			else if((p_node)->parent->leftchild == (p_node))
			{
				(p_node)->parent->leftchild = (p_node)->leftchild;
				(p_node)->leftchild->parent = (p_node)->parent;
				free((p_node));
			}
		}

		//when both child are not NULL
		if((p_node)->rightchild != NULL && (p_node)->leftchild != NULL)
		{
			if((p_node)->parent->rightchild == (p_node))
			{
				//(*pp_node)->parent->rightchild = NULL;
				(p_node)->parent->rightchild = (p_node)->rightchild;
				//temp = (*pp_node)->parent;
				//temp.rightchild = (*pp_node)->rightchild;
				insert_for_delete(((p_node)->rightchild),(p_node)->leftchild);
				free((p_node));
				
			}
			else if((p_node)->parent->leftchild == (p_node))
			{
				//(*pp_node)->parent->leftchild = NULL;
				(p_node)->parent->leftchild = (p_node)->rightchild;
				insert_for_delete(((p_node)->rightchild),(p_node)->leftchild);
				free((p_node));
			}
		}
	}
	else
	{
		if((p_node)->data < number)
		{
			delete_node(p_node->rightchild,number);	
		}
		
		if((p_node)->data > number)
		{
			delete_node(p_node->leftchild,number);
		}
	}
}

free_tree.c

/*******************************************************************************
* code writer: EOF
* Date : 2014.02.20
* code purpose:
		This code is my implementation for function -- free_tree
*e-mail:[email protected]

If there somthing wrong with my code, please touch me by e-mail.Thank you!
*****************************************************************************/
#include<stdio.h>
#include<stdlib.h>
#include "bst.h"

void free_tree(struct node* p_node)// use recursion to free the memory we allocated
{
	if(p_node->leftchild == NULL && p_node->rightchild == NULL)
	{
		free(p_node);
		p_node = NULL;
	}
	else if(p_node->leftchild != NULL && p_node->rightchild == NULL)
	{
		free_tree(p_node->leftchild);	
	}
	else if(p_node->leftchild == NULL && p_node->rightchild != NULL)  
	{
		free_tree(p_node->rightchild);
	}
	else if (p_node->leftchild != NULL && p_node->rightchild != NULL)
	{
		free_tree(p_node->rightchild);
		free_tree(p_node->leftchild);	
	}
	
}

print_tree.c

/*******************************************************************************
* code writer: EOF
* Date : 2014.02.20
* code purpose:
		This code is the definition for function -- print_tree
*e-mail:[email protected]

If there somthing wrong with my code, please touch me by e-mail.Thank you!
*****************************************************************************/
#include "bst.h"
#include "stdio.h"

int print_node(struct node* p_node)// use recursion to print out the data in the binary tree
{
	// print the left side of the binary tree
	if(p_node->leftchild != NULL)
	{
		print_node(p_node->leftchild);
	}
	printf("%d\n",p_node->data);

	// print the right side of the binary tree
	if(p_node->rightchild != NULL)
	{
		print_node(p_node->rightchild);
	}
	//printf("%d\n",p_node->data); we don't need this 
}

学习感想：

1.知道二叉树很长时间了，但是一直没有实现，多次失败，感觉懂了，但是就是实现不了。这次搞定了。有些事就是要死磕，一次不行再来一次。

2.递归真的很重要！很多算法的实现都是用递归，而我往往有点对递归没好感，是自己不熟悉的原因吧，用的少。

3.我始终认为，任何事情，只有真的做到了，才叫学会，所以我死磕。

loving you, tree...................

2014.02.27

前些天大体实现了BST，但是还是忘记实现删除节点了。现在更新实现了删除节点的source files.

实现delete_node.c的时候还是遇到了一个bug。搞了两天才搞明白，还好没有到寝食难安的地步，只是每次走在路上

都想这个问题，问题最后搞清楚了，最后的建议就是没事API的参数少用二级指针，今天听学长说，你会用,

别人就不一定看得懂了，代码的易读性和可维护性就降低了，而且用的少容易出bug. 

这次这个bug主要是二级指针传递的时候就是传递了指向了结构体指针的地址，后面就导致了奇怪的bug出现.

教训：

分析问题，不光是要从上面找啊，还要分析语句的后面，递归的时候特别要注意。

所有的bug都是有逻辑的, 自己要冷静思考不要陷入理想思维.

2014.01.26

原来的代码丢失insert_node()这个函数的实现，现在更新了函数实现...对今天之前的版本有少许改动，去掉了二级指针的使用

2015.01.28

添加了Python实现

                                     第二田径场的陌生人