Deep Learning 系列（3）：CNN（卷积神经网络）

早就想写CNN的博文了，最近刚好有空。总体来说，CNN框架不难理解，关键是里面的实现细节值得思考。初次了解，可以先看看UFLDL教程中的Convolution和Pooling。

这基本上是CNN的核心。

简单理解：Convolution即用一个滑动的小窗口去卷积一个大的图像。

          Pooling 即滑动的小窗口各权值为1/m  (m 为权值个数)。

另外，在pooling中有sigmoid激活函数，进行非线性化。

zouxy09 对CNN框架有详细描述。

Tornadomeet对重点对C3层与S2层的特征图链接有详细描述。

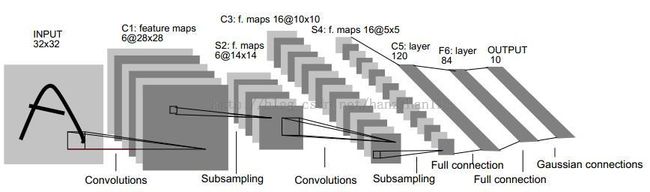
下图为经典的LeNet5结构图。

C1层，由6个filter（5*5）卷积Input 32*32得到。6@（32-5+1）*（32-5+1）。参数有6*（5*5+1）=156个。1为偏置bias。

S2层，对C1进行池化和sigm非参数化。6@（28/2）*（28/2）。参数有6*（1+1）=12。两个1分别为权值W_s2和偏置b_s2。

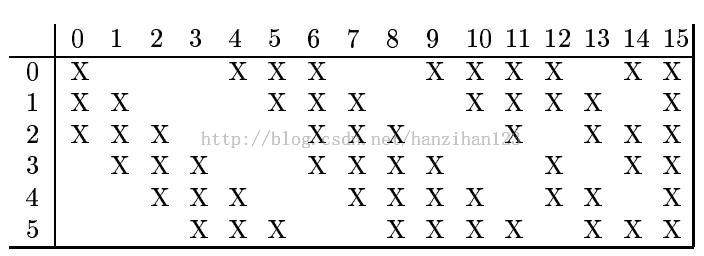
C3层，可参考下表：

X代表C3层中与S2层有连接的。

Tornadomeet写的有点复杂，我的理解是：C3中有16个filter，用他们分别去卷积S2中与之有连接的特征图。如C3中No.3与S2中No.3/4/5有连接，则用No.3号filter去卷积这三个特征图，然后求和。

S4层同S2。

C5层同C3，但不同的是有120个filter，分别去卷积S4层中全部16个特征图。

F6层与C5是全连接，即分别与C5层中120个特征图相连。采用sigm激活函数。

 

具体代码，参见DeepLearnToolbox  

\tests\test_example_CNN.m

该代码没用到tornadomeet的博文表，而是直接与S2全部6个特征图卷积。

代码详解可参见Dark的CNN博文。

这里只对一些关键处作解释~

// cnntrain.m, 其中code 12-23

for l = 1 : numbatches     %批量梯度下降的次数
            batch_x = x(:, :, kk((l - 1) * opts.batchsize + 1 : l * opts.batchsize)); % 这里是随机提取样本中的batchsize个样本，作批量梯度下降法
            batch_y = y(:,    kk((l - 1) * opts.batchsize + 1 : l * opts.batchsize));

            net = cnnff(net, batch_x); %前向传导
            net = cnnbp(net, batch_y); %后项调参
            net = cnnapplygrads(net, opts); %更新权值
            if isempty(net.rL)
                net.rL(1) = net.L;
            end
            net.rL(end + 1) = 0.99 * net.rL(end) + 0.01 * net.L;
        end

// cnnff.m, 全部code吧~（将算法表述的很好， 值得借鉴！）

function net = cnnff(net, x)
    n = numel(net.layers);
    net.layers{1}.a{1} = x;
    inputmaps = 1;

    for l = 2 : n   %  for each layer
        if strcmp(net.layers{l}.type, 'c')
            %  !!below can probably be handled by insane matrix operations
            for j = 1 : net.layers{l}.outputmaps   %  for each output map
                %  create temp output map
                z = zeros(size(net.layers{l - 1}.a{1}) - [net.layers{l}.kernelsize - 1 net.layers{l}.kernelsize - 1 0]);
                for i = 1 : inputmaps   %  for each input map
                    %  注意将每一个input特征图与K核卷积，求和为output特征图。K核有inputmaps * outputmaps个
                    z = z + convn(net.layers{l - 1}.a{i}, net.layers{l}.k{i}{j}, 'valid');
                end
                %  添加bias，用sigm非线性化
                net.layers{l}.a{j} = sigm(z + net.layers{l}.b{j});
            end
            %  set number of input maps to this layers number of outputmaps
            inputmaps = net.layers{l}.outputmaps;
        elseif strcmp(net.layers{l}.type, 's')
            %  downsample
            for j = 1 : inputmaps
                % 这里重要，用convn 作pooling，简洁！
                z = convn(net.layers{l - 1}.a{j}, ones(net.layers{l}.scale) / (net.layers{l}.scale ^ 2), 'valid');   %  !! replace with variable
                net.layers{l}.a{j} = z(1 : net.layers{l}.scale : end, 1 : net.layers{l}.scale : end, :);
            end
        end
    end

    %  concatenate all end layer feature maps into vector
    net.fv = [];
    for j = 1 : numel(net.layers{n}.a)
        sa = size(net.layers{n}.a{j});
        % 这里是直接拉伸为向量，每个样本的特征大小为layer{n}层特征图个数* sa(1) * sa(2)
        net.fv = [net.fv; reshape(net.layers{n}.a{j}, sa(1) * sa(2), sa(3))];
    end
    %  前馈给感知机，这里是权值ffw
    net.o = sigm(net.ffW * net.fv + repmat(net.ffb, 1, size(net.fv, 2)));

end

//cnnbp.m, 全部code吧~（这里其实就是反向传导算法！）

function net = cnnbp(net, y)
    n = numel(net.layers);

    %   error
    net.e = net.o - y;
    %  loss function
    net.L = 1/2* sum(net.e(:) .^ 2) / size(net.e, 2);

    %%  backprop deltas
    net.od = net.e .* (net.o .* (1 - net.o));   %  output delta
    net.fvd = (net.ffW' * net.od);              %  feature vector delta
    if strcmp(net.layers{n}.type, 'c')         %  only conv layers has sigm function
        net.fvd = net.fvd .* (net.fv .* (1 - net.fv));
    end

    %  reshape feature vector deltas into output map style
    sa = size(net.layers{n}.a{1});
    fvnum = sa(1) * sa(2);
    for j = 1 : numel(net.layers{n}.a)
        net.layers{n}.d{j} = reshape(net.fvd(((j - 1) * fvnum + 1) : j * fvnum, :), sa(1), sa(2), sa(3));
    end

    for l = (n - 1) : -1 : 1
        if strcmp(net.layers{l}.type, 'c')
            for j = 1 : numel(net.layers{l}.a)
                net.layers{l}.d{j} = net.layers{l}.a{j} .* (1 - net.layers{l}.a{j}) .* (expand(net.layers{l + 1}.d{j}, [net.layers{l + 1}.scale net.layers{l + 1}.scale 1]) / net.layers{l + 1}.scale ^ 2);
            end
        elseif strcmp(net.layers{l}.type, 's')
            for i = 1 : numel(net.layers{l}.a)
                z = zeros(size(net.layers{l}.a{1}));
                for j = 1 : numel(net.layers{l + 1}.a)
                     z = z + convn(net.layers{l + 1}.d{j}, rot180(net.layers{l + 1}.k{i}{j}), 'full');
                end
                net.layers{l}.d{i} = z;
            end
        end
    end

    %%  calc gradients
    for l = 2 : n
        if strcmp(net.layers{l}.type, 'c')
            for j = 1 : numel(net.layers{l}.a)
                for i = 1 : numel(net.layers{l - 1}.a)
                    net.layers{l}.dk{i}{j} = convn(flipall(net.layers{l - 1}.a{i}), net.layers{l}.d{j}, 'valid') / size(net.layers{l}.d{j}, 3);
                end
                net.layers{l}.db{j} = sum(net.layers{l}.d{j}(:)) / size(net.layers{l}.d{j}, 3);
            end
        end
    end
    net.dffW = net.od * (net.fv)' / size(net.od, 2);
    net.dffb = mean(net.od, 2);

    function X = rot180(X)
        X = flipdim(flipdim(X, 1), 2);
    end
end

更详细可参见：refer-2 这篇论文已经UFLDL中的反向传导算法

其本质跟DBN是同样的，需要用BP来进行反向fine。不同的可能是实现细节上，因为有pooling层（无sigm），则code的实现细节有变化。当然这个代码真心写的很好！

参考：

1.  Convolutional Neural Networks (LeNet)

2. Notes on Convolutional Neural Networks

3. ImageNet Classification with Deep Convolutional Neural Networks

4. zouxy09 的博文 （对CNN有详细的描述）

5. tornadomeet 的博文 （对S2-C3的组合特征有描述）

6. Dar 的博文 （对DL-tool工具箱的CNN有描述）

未完待续。。。