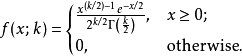卡方分布（chi-square distribution, χ²-distribution）是概率论与统计学中常用的一种概率分布。k个独立的标准正态分布变量的平方和服从自由度为k的卡方分布。卡方分布是一种特殊的伽玛分布，是统计推断中应用最为广泛的概率分布之一，例如假设检验和置信区间的计算。
若k个随机变量、……、是相互独立，符合标准正态分布的随机变量（数学期望为0、方差为1），则随机变量Z的平方和
-
被称为服从自由度为 k 的卡方分布，记作
-
-
概率密度函数
期望和方差
分布的
均值为自由度 n，记为 E(
) = n。
分布的
方差为2倍的自由度(2n)，记为 D(
) = 2n。
性质
1)
分布在第一
象限内，卡方值都是正值，呈正偏态（右偏态），随着参数 n 的增大，
分布趋近于正态分布；卡方分布密度曲线下的面积都是1.
2)
分布的均值与
方差可以看出，随着自由度n的增大，χ2分布向
正无穷方向延伸（因为均值n越来越大），分布
曲线也越来越低阔（因为方差2n越来越大）。
3）不同的自由度决定不同的卡方分布，自由度越小，分布越偏斜。
累积分布函数
卡方分布的累积分布函数为：
- ，
其中γ(k,z)为不完全Gamma函数
在大多数涉及卡方分布的书中都会提供它的累积分布函数的对照表。此外许多表格计算软件如OpenOffice.org Calc和Microsoft Excel中都包括卡方分布函数。
自由度为k的卡方变量的平均值是k，方差是2k。 卡方分布是伽玛分布的一个特例，它的熵为：
-
其中是双伽玛函数。
伽玛函数（Gamma Function）作为
阶乘的延拓，是定义在复数范围内的
亚纯函数，通常写成
。
在实数域上伽玛函数定义为：
在复数域上伽玛函数定义为：
其中
，此定义可以用
解析开拓原理拓展到整个
复数域上，非正整数除外。
标准正态分布又称为u分布，是以0为
均数、以1为
标准差的正态分布，记为N（0，1）。
标准正态分布曲线下面积分布规律是：在-1.96～+1.96范围内曲线下的面积等于0.9500，在-2.58～+2.58范围内曲线下面积为0.9900。统计学家还制定了一张统计用表（自由度为∞时），借助该表就可以估计出某些特殊u1和u2值范围内的曲线下面积。
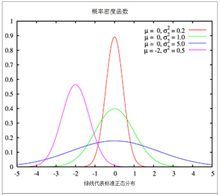
正态分布的概率密度函数曲线呈钟形，因此人们又经常称之为
钟形曲线。我们通常所说的
标准正态分布是位置参数
均数为0, 尺度参数：
标准差为1的正态分布（见右图中绿色曲线）。
正态分布中一些值得注意的量：
密度函数关于平均值对称
平均值与它的
众数（statistical mode）以及
中位数（median）同一数值。
函数曲线下68.268949%的面积在平均数左右的一个
标准差范围内。
95.449974%的面积在平均数左右两个标准差的范围内。
99.730020%的面积在平均数左右三个标准差的范围内。
99.993666%的面积在平均数左右四个标准差的范围内。
函数曲线的反曲点（inflection point）为离平均数一个标准差距离的位置。
非中心卡方分布
[1]
[2]
是有正态分布衍生得到的一个概率分布. 设
![X_1,X_2,\cdots,X_n]( "X_1,X_2,\cdots,X_n")
为一组独立的随机变量, 并且
![X_i\sim N(\mu_i,1),i=1,2,\cdots,n]( "X_i\sim N(\mu_i,1),i=1,2,\cdots,n")
(
![X_i]( "X_i")
服从
正态分布
), 定义随机变量
![\xi=\Sigma_{i=1}^nX_i^2]( "\xi=\Sigma_{i=1}^nX_i^2")
, 称随机变量
![\xi]( "\xi")
服从自由度为
![n]( "n")
, 非中心参数为
![\delta]( "\delta")
的的非中心卡方分布, 记为
![\xi\sim \chi_{n,\delta}^2]( "\xi\sim \chi_{n,\delta}^2")
; 其中
![\delta=\sqrt{\Sigma_{i=1}^n\mu_i^2}]( "\delta=\sqrt{\Sigma_{i=1}^n\mu_i^2}")
. 当
![\delta=0]( "\delta=0")
时, 随机变量
![\xi]( "\xi")
服从自由度为
![n]( "n")
的
卡方分布
.
SAS设定自由度和非中心参数计算p分位点的方式如下：
272 data _null_;
273 q=cinv(0.95,10,25.2);*0.95分位数,自由度为10，非中心参数为25.2;
274 put q=;
275 run;
q=54.759186647
NOTE: “DATA 语句”所用时间（总处理时间）:
实际时间 0.00 秒
CPU 时间 0.00 秒
Required Arguments
p
is a numeric probability.
df
is a numeric degrees of freedom parameter.
Optional Argument
nc
is a numeric noncentrality parameter.
Details
The CINV function returns the
p
th quantile from the chi-square distribution with degrees of freedom
df and a noncentrality parameter
nc. The probability that an observation from a chi-square distribution is less than or equal to the returned quantile is
p. This function accepts a noninteger degrees of freedom parameter
df.
If the optional parameter
nc is not specified or has the value 0, the quantile from the central chi-square distribution is returned. The noncentrality parameter
nc is defined such that if X is a normal random variable with mean
μ and variance 1, X
2 has a noncentral chi-square distribution with
df=1 and
nc = μ
2.
总体正态分布的等距分组的组距确定，即组距相等。
n=1+3.322*LOG(N)
d=R/n
N:总体容量
n:组数
R：总体全距：最大值与最小值之差。
d:组距
data _null_;
N=1000;
n=1+3.322*LOG(N);
mymax=18651;
mymin=1240;
r=mymax-mymin;
d=r/n;
put d;
run;
