桶排序(Bucket Sort),基数排序(Radix_Sort)

<算法导论>第八章3 桶排序(Bucket Sort)

2011-12-23 14:34

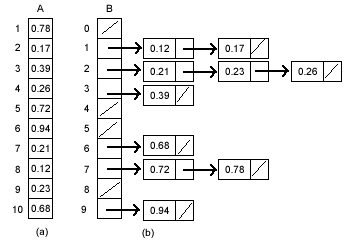
假设有一组长度为N的待排关键字序列K[1....n]，首先将这个序列划分成M个的子区间(桶) 。然后基于某种映射函数，将待排序列的关键字k映射到第i个桶中(即桶数组B的下标 i)，那么该关键字k就作为B[i]中的元素(每个桶B[i]都是一组大小为N/M的序列)。接着对每个桶B[i]中的所有元素进行比较排序(可以使用快排)。然后依次枚举输出B[0]....B[M]中的全部内容即是一个有序序列。 比如考试分数通常为0-100分，我们可以建立11个桶，然后确定映射函数f(k)=k/10。则分数49将定位到第4个桶中(49/10=4)。 桶排序的f(k)值的计算，其作用就相当于快排中划分，已经把大量数据分割成了基本有序的数据块(桶)。然后只需要对桶中的少量数据做先进的比较排序即可。应该尽量做到以下两点: (1) 映射函数f(k)能够将N个数据平均的分配到M个桶中，这样每个桶就有[N/M]个数据量。 (2) 尽量的增大桶的数量。极限情况下每个桶只能得到一个数据，这样就完全避开了桶内数据的“比较”排序操作。当然，做到这一点很不容易，数据量巨大的情况下，f(k)函数会使得桶集合的数量巨大，空间浪费严重。这就是一个时间代价和空间代价的权衡问题了。 void BucketSort(int *A,int size) {     vector<int> Bucket[11];     memset(Bucket,0,sizeof(0));     int i,j,k,D,key;     for(i=0;i<size;++i)//将每个元素插入到相应的桶中     {         key = A[i];         D = key/10; //桶下标         j = Bucket[D].size()-1;         Bucket[D].push_back(key);         while(j>=0 && Bucket[D][j]>key)//插入排序         {             swap(Bucket[D][j],Bucket[D][j+1]);             --j;         }     }     k = 0;     for(i=0;i<11;++i)         for(j=0;j<Bucket[i].size();++j)         A[k++] = Bucket[i][j]; } void TestBucketSort() {     int A[] = {15,76,21,90,64,8,88,31,57,49};     cout<<"Init A:\n";     copy(A,A+10,ostream_iterator<int>(cout," "));     cout<<endl;     BucketSort(A,10);     cout<<"After BucketSort A:\n";     copy(A,A+10,ostream_iterator<int>(cout," "));     cout<<endl; } +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ +++++++++++++++++++++++++++ +Grant推荐：                                            + +不错的博客地址：http://blog.csdn.net/kay_sprint/article/category/851272     + + 关注标签 1.Data Structure(54)  2.  Algorithm (79)   3.  C++ Note (21)               + +++++++++++++++++++++++++++ Bucket_Sort and Radix_Sort 分类： Data Structure Algorithm 2011-08-22 17:16  51人阅读  评论(0)  收藏  举报 这个是原文地址 点此连接。   桶式排序 桶式排序的原理是：利用待排序序列元素的值作为新序列的索引进行插入，完成新序列的建立后，只需对新序列进行遍历即可完成排序（具体遍历过程和新序列元素的值有关） 假设有N个整数的序列，范围从0到M-1。现建立一个名为Count的桶序列，长度为M，并初始化为0。于是，Count有M个桶，开始时都是空的。对待排序序列进行遍历，当遍历至原序列元素Ai时，Count[Ai]增1。Count序列建立完毕后，对其进行遍历，遍历输出的不是Count序列元素的值，而是其索引，每个索引输出的次数由其对应元素的值决定，元素值为0则不输出 代码 #include<iostream> using namespace std; void bucket_sort(int m, int n, int a[]) { //m为待排序序列元素值取范的上限（下限默认为0），n为序列长度，a为原序列 int *b=new int[m]; //注意新序列长度不是n而是m for(int i=0;i<m;i++) //初始化 b[i]=0; for(i=0;i<n;i++) //由原序列获得新序列 b[a[i]]++; int j; for(i=0,j=0;i<m;i++) { //输出新序列 if(b[i]!=0) { for(int k=0;k<b[i];k++) { a[j]=i; j++; } } } } int main() { int a[10]={8,65,23,5,56,9,23,56,99,12}; bucket_sort(100,10,a); for(int i=0;i<10;i++) cout<<a[i]<<" "; cout<<endl; return 0; } 桶式排序的局限性在于 待排序序列元素的值只能为整数 若待排序序列元素值的取值范围很大，则Count序列需占用很大空间，而实际上得到的Count序列是很稀疏的   基数排序 相比于桶式排序，基数排序仍只适用于元素值为整数的序列，但它的Count序列空间占用比桶式排序小得多 基数排序是桶式排序的推广，设待排序序列长度为M，取值范围为0到N^p-1，N即为基数，p为指数。对于基数排序，我们只需要一个长度为N的Count序列和p趟排序即可完成 我们进行p趟排序，每次以元素值的某一“位”（对基数N所取的位，基数为10时就是一般定义上的位）为关键字进行排序，每趟都是一次桶式排序，顺序必须是先从最低“位”开始排序，最后对最高“位”排序 根据上述分析，相比于桶式排序，基数排序有以下特性 Count序列是一个二维矩阵，大小为N×M（一般来说，其空间占用远小于桶式排序） 桶式排序的Count序列是一维列表，这是因为同一桶内的元素的值必定相同；而基数排序的同一桶内的元素只是针对该趟对应的“位”相同，元素值不一定相同，因此桶还需要一定的“高度”来记录不同的元素值，以免混淆 实际应用中，N和p是可以任意取值的，只要保证待排序序列的取值范围为0到N^p-1即可。但另一方面，基数N决定了空间复杂度，指数p决定了时间复杂度，需要一定平衡 代码 #include<iostream> #include<math.h> using namespace std; void radix_sort(int m, int n, int p, int a[]) { //m代表待排序序列长度，n代表基数，p代表元素最大的位数，a代表待排序序列 int **b=new int*[n]; //b代表count序列 for(int i=0; i<n;i++) b[i]=new int[m]; for(int t=1;t<=p;t++) { //p趟排序 for(i=0;i<n;i++) { //每趟都要对count序列初始化为0 for(int j=0;j<m;j++) { b[i][j]=0; } } int *c=new int[n]; //记录桶的高度 for(int x=0;x<n;x++) c[x]=0; for(int j=0; j<m;j++) { int k=(a[j]%(int)pow(n,t))/pow(n,t-1); //关键：获得该趟对应的“位”，根据该“位”将元素放入对应的桶中 b[k][c[k]]=a[j]; c[k]++; //同时要增加对应桶的高度 } int k=0; for(int i=0; i<n; i++) { //单趟cnt序列建立完毕后，将其输出回序列a，以便下一趟的排序 for(int j=0;j<c[i]; j++) { a[k]=b[i][j]; k++; } } } } int main() { int a[8]={1183,1263,2574,92,5447,3988,6774,8474}; int m=8; int n=10; int p=4; radix_sort(m,n,p,a); for(int i=0;i<8;i++) cout<<a[i]<<" "; cout<<endl; return 0; } +++++++++++++++++++++++++++++++++++++++++++++++++++++++++ +++++++++++++++++++++++++++ +Grant推荐：                                            + +不错的博客地址：http://blog.csdn.net/taesimple/article/category/783267     + + 关注标签 1. Algorithm(14)  2.  Linux (26)  3.  Shell (13)           + +++++++++++++++++++++++++++   基数排序（radix sort）总结 分类： Algorithm 2011-07-18 20:41  86人阅读  评论(0)  收藏  举报 讨论基数排序之前，先来看名为“桶式排序”的方法 桶式排序 桶式排序的原理是：利用待排序序列元素的值作为新序列的索引进行插入，完成新序列的建立后，只需对新序列进行遍历即可完成排序（具体遍历过程和新序列元素的值有关） 假设有N个整数的序列，范围从0到M-1。现建立一个名为Count的桶序列，长度为M，并初始化为0。于是，Count有M个桶，开始时都是空的。对待排序序列进行遍历，当遍历至原序列元素Ai时，Count[Ai]增1。Count序列建立完毕后，对其进行遍历，遍历输出的不是Count序列元素的值，而是其索引，每个索引输出的次数由其对应元素的值决定，元素值为0则不输出 代码如下 void bucket_sort(int m, int n, int * a){ //m为待排序序列元素值取范的上限（下限默认为0），n为序列长度，a为原序列 int * b = malloc(m*sizeof(int)); //注意新序列长度不是n而是m for(int i = 0; i < m; i++) //初始化 b[i] = 0; for(int i = 0; i < n; i++) //由原序列获得新序列 b[a[i]]++; for(int i = 0, j = 0; i < m; i++){ //输出新序列 if(b[i] != 0){ for(int k = 0; k < b[i]; k++){ a[j] = i; j++; } } } } 桶式排序的局限性在于 待排序序列元素的值只能为整数 若待排序序列元素值的取值范围很大，则Count序列需占用很大空间，而实际上得到的Count序列是很稀疏的 基数排序 相比于桶式排序，基数排序仍只适用于元素值为整数的序列，但它的Count序列空间占用比桶式排序小得多 基数排序是桶式排序的推广，设待排序序列长度为M，取值范围为0到N^p-1，N即为基数，p为指数。对于基数排序，我们只需要一个长度为N的Count序列和p趟排序即可完成 我们进行p趟排序，每次以元素值的某一“位”（对基数N所取的位，基数为10时就是一般定义上的位）为关键字进行排序，每趟都是一次桶式排序，顺序必须是先从最低“位”开始排序，最后对最高“位”排序 对于”先低位，后高位“原则，作如下理解：低位的排序结果会影响两个高位相同元素的排序。譬如21和27，第一趟排序时，21所在桶位于27所在桶之前，因此第二趟排序时会先扫描到21。最终结果是，第二趟排序结束后21在27之前 根据上述分析，相比于桶式排序，基数排序有以下特性 Count序列是一个二维矩阵，大小为N×M（一般来说，其空间占用远小于桶式排序） 桶式排序的Count序列是一维列表，这是因为同一桶内的元素的值必定相同；而基数排序的同一桶内的元素只是针对该趟对应的“位”相同，元素值不一定相同，因此桶还需要一定的“高度”来记录不同的元素值，以免混淆 实际应用中，N和p是可以任意取值的，只要保证待排序序列的取值范围为0到N^p-1即可。但另一方面，基数N决定了空间复杂度，指数p决定了时间复杂度，需要一定平衡 代码如下（任意基数） void radix_sort(int m, int n, int p, int * a){ //m代表待排序序列长度，n代表基数，p代表指数，a代表待排序序列 int ** b = (int **)malloc(n*sizeof(int *)); //b代表count序列 for(int i = 0; i < n; i++) b[i] = (int *)malloc(m*sizeof(int)); for(int t = 1; t <= p; t++){ //p趟排序 int * c = (int *)malloc(n*sizeof(int)); //记录桶的高度 memset(c, 0, n*sizeof(int)); //每趟都要将桶高数组c初始化为0 for(int j = 0; j < m; j++){ int k = (a[j]%(int)pow(n, t))/pow(n, t-1); //关键：获得该趟对应的“位”，根据该“位”将元素放入对应的桶中 b[k][c[k]] = a[j]; c[k]++; //同时要增加对应桶的高度 } int k = 0; for(int i = 0; i < n; i++) //单趟cnt序列建立完毕后，将其输出回序列a，以便下一趟的排序 for(int j = 0; j < c[i]; j++) a[k++] = b[i][j]; } } 代码如下（以10为基数） void radix_sort(int a[], int n, int m){ //n为待排序数组长度，m为待排序数组取范上限的“位数” int ** b = (int **)malloc(10*sizeof(int *)); for(int i = 0; i < 10; i++) b[i] = (int *)malloc(n*sizeof(int)); int * c = (int *)malloc(10*sizeof(int)); for(int t = 0; t < m; t++){ memset(c, 0, 10*sizeof(int)); for(int i = 0; i < n; i++){ int k = a[i]%(int)pow(10, t+1)/pow(10, t); b[k][c[k]] = a[i]; c[k]++; } int k = 0; for(int i = 0; i < 10; i++) for(int j = 0; j < c[i]; j++) a[k++] = b[i][j]; } } 上一篇：poj 1159（动态规划）