一起talk C栗子吧（第四十一回：C语言实例--哈夫曼树）

各位看官们，大家好，上一回中咱们说的是遍历二叉树的例子，这一回咱们说的例子是：哈夫曼树。闲话

休提，言归正转。让我们一起talk C栗子吧！

哈夫曼树也叫赫夫曼树，其实它们都是从英语翻译过来的，只是音译的不同而已，大家不需要对它咬文嚼

字。它的英文原文是：Huffman.这是一个数学家的姓氏，因为它发明了哈夫曼编码，为了纪念他所做贡

献，所以用它的姓氏命名。

在说哈夫曼树前，我们说一下树的路径和权。树中结点的路径是指从树中根结点到某个结点的距离，如果

为这个路径加上一个权值，那么结点的带权路径就是路径长度与权值的乘积。树的带权路径是指树中所有

结点的带权路径之和。这么说，大家可能觉得很抽象，我们举个例子来说明：

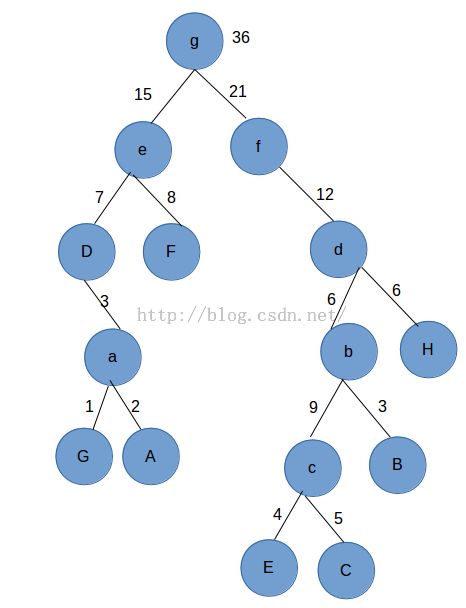
在上面的图中，我们依次列出个结点的路径：

• Path-A：2 ==>从根结点g到A的路径为4，权值设定为2,带权路径为4×2=8；
• Path-B：3 ==>从根结点g到B的路径为4，权值设定为3,带权路径为4×3=12；
• Path-C：5 ==>从根结点g到C的路径为5，权值设定为5,带权路径为5×5=25；
• Path-D：7 ==>从根结点g到D的路径为2，权值设定为7,带权路径为2×7=14；
• Path-E：4 ==>从根结点g到E的路径为5，权值设定为4,带权路径为5×4=20；
• Path-F：8 ==>从根结点g到F的路径为2，权值设定为8,带权路径为2×8=16；
• Path-G：1 ==>从根结点g到G的路径为4，权值设定为1,带权路径为4×1=5；
• Path-H：6 ==>从根结点g到H的路径为3，权值设定为6,带权路径为3×6=18；
• 这棵树的带权路径等于：Path-A+Path-B+..Path-H=8+12+25+14+20+16+5+18=118

在计算的过程中，小写字母所在的结点是合成的结点，因此不统计它们的权值。或者把它们理解成构造哈

夫曼树的辅助结点，就像现实生活中的临时工，那么其它的结点就是正式工了。哈哈！

通过这个例子，我想大家已经明白了树的带权路径。接下来我们说说什么是哈夫曼树。哈夫曼树是一种带

权路径长度最小的二叉树。创建哈夫曼树的思路为：把二叉树中权值最小的两个结点当作左右孩子，其中

左边孩子的权值更加小一些；接着把这两个孩子的权值相加当作它们父亲的权值；然后把这两个孩子从二

叉树中删除，同时把它们的父亲放到二叉树中；反复执行这个过程，直到二叉树中只剩下最后一个结点为

止，这个时候的二叉树就是一棵哈夫曼树。看官们，这个思路可能抽象一些，我们顺着这个思路来说说如

何创建哈夫曼树，下面是具体的实现步骤：

• 1.从终端或者文件中读取结点的值，把这些存放在一个数组中；
• 2.把数组中的元素，依据结点的权值从小到大进行排序；
• 3.从数组中获取元素，获取数组中的第一个元素就可以；
• 4.判断获取的值，如果值是‘X’，那么表示二叉树中没有结点，返回步骤3.如果不是‘X’，进入步骤5；
• 5.给结点分配存储空间，并且把步骤3中获取元素的值当作该结点的值；
• 6.重复步骤3到5,获取第二个元素；
• 7.把数组中前两个元素删除，并且合成为一个新元素，新元素的权值为这两个元素权值之和；被删除的这
• 两个元素是新元素的左孩子和右孩子，其中权值小的是左孩子；
• 8.把步骤7中的新元素放到数组中第一个位置，其它元素向前移动一位；
• 9.反复执行步骤2到8,直到数组中只剩下一个元素为止。
• 
  

看官们，正文中就不写代码了，详细的代码放到了我的资源中，大家可以点击这里下载使用。在代码中把

元素的值和权值都放到了一个数组中。数组排序的过程封装成了一个函数，同时还把步骤7和8中生成父结

点的过程封装成了一个函数。这样可以提高代码的复用性。另外，大家还记得我们在前面章回中创建普通

二叉树的过程吧，我建议大家对比一下创建普通二叉树的过程和创建哈夫曼树的过程。你会发现创建普通

二叉树是从树的根结点开始一直到叶子结点，专业上叫作自顶向下；而哈夫曼树正好与它相反：从叶子结

点开始一直到根结点，专业上叫作自底向上。下面是生成生成Huffman树的过程，我在每行末尾添加了相

关的注释，方便大家理解 。

The inputting value of node are as following

A  2 |B  3 |C  5 |D  7 |E  4 |F  8 |G  1 |H  6 |

Create a Huffman Tree

//下面是创建Huffman树过程中，结点序列的变化，其中X表示空结点，其权值为0

G  1 |A  2 |B  3 |E  4 |C  5 |H  6 |D  7 |F  8 | //第一次排序后结点序列

a  3 |B  3 |E  4 |C  5 |H  6 |D  7 |F  8 |X  0 | //第一次合并后的结点序列

a  3 |B  3 |E  4 |C  5 |H  6 |D  7 |F  8 |X  0 | //第二次排序后结点序列

b  6 |E  4 |C  5 |H  6 |D  7 |F  8 |X  0 |X  0 | //第二次合并后的结点序列

E  4 |C  5 |b  6 |H  6 |D  7 |F  8 |X  0 |X  0 | //第三次排序后结点序列

c  9 |b  6 |H  6 |D  7 |F  8 |X  0 |X  0 |X  0 | //第三次合并后的结点序列

b  6 |H  6 |D  7 |F  8 |c  9 |X  0 |X  0 |X  0 | //第三次排序后结点序列

d 12 |D  7 |F  8 |c  9 |X  0 |X  0 |X  0 |X  0 | //第三次合并后的结点序列

D  7 |F  8 |c  9 |d 12 |X  0 |X  0 |X  0 |X  0 | //第四次排序后结点序列

e 15 |c  9 |d 12 |X  0 |X  0 |X  0 |X  0 |X  0 | //第四次合并后的结点序列

c  9 |d 12 |e 15 |X  0 |X  0 |X  0 |X  0 |X  0 | //第五次排序后结点序列

f 21 |e 15 |X  0 |X  0 |X  0 |X  0 |X  0 |X  0 | //第五次合并后的结点序列

e 15 |f 21 |X  0 |X  0 |X  0 |X  0 |X  0 |X  0 | //第六次排序后结点序列

g 36 |X  0 |X  0 |X  0 |X  0 |X  0 |X  0 |X  0 | //第六次合并后的结点序列

g 36 |X  0 |X  0 |X  0 |X  0 |X  0 |X  0 |X  0 | //第七次只排序，因为只有一个结点


Traverse a Huffman Tree

g e D F f c E C d b a G A B H   //前序遍历Huffman树的结果

Destroy a Huffman Tree 

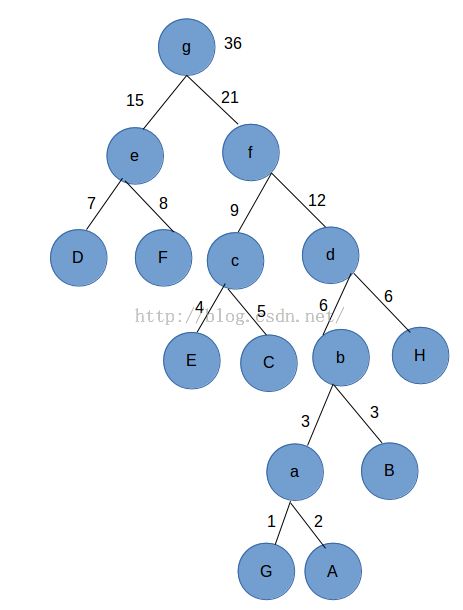
下面是刚才图中哪棵树的哈夫曼树，我们一起来计算一下这棵Huffman树的权值：

• Path-A：2 ==>从根结点g到A的路径为5，权值设定为2,带权路径为5×2=10；
• Path-B：3 ==>从根结点g到B的路径为4，权值设定为3,带权路径为4×3=12；
• Path-C：5 ==>从根结点g到C的路径为3，权值设定为5,带权路径为3×5=15；
• Path-D：7 ==>从根结点g到D的路径为2，权值设定为7,带权路径为2×7=14；
• Path-E：4 ==>从根结点g到E的路径为3，权值设定为4,带权路径为3×4=12；
• Path-F：8 ==>从根结点g到F的路径为2，权值设定为8,带权路径为2×8=16；
• Path-G：1 ==>从根结点g到G的路径为5，权值设定为1,带权路径为5×1=5；
• Path-H：6 ==>从根结点g到H的路径为3，权值设定为6,带权路径为3×6=18；
• 这棵树的带权路径等于：Path-A+Path-B+..Path-H=10+12+15+14+12+16+5+18=102

对比一下两棵树的带权路径就能发现Huffman树的带权路径要比普通树的小。因此，我们说哈夫曼树是带

权路径最小的二叉树。

各位看官，关于哈夫曼树的例子咱们就说到这里。欲知后面还有什么例子，且听下回分解。