poj3020-二分图匹配

对于任意图：

|最小边覆盖|+|最大匹配|=|V|

二分图的最大匹配=最小点覆盖数

对于二分图：

以下数值等价.

最大匹配

最小点覆盖

|V|-最大独立集(二分图or有向无环图)

|V|-最小边覆盖数

|V|-最小路径覆盖数(有向无环图)

|V|-最小路径覆盖数/2(无向图)

（上面括号里有有向无环图的，均是将一个点拆成两个点连边匹配）

由于任意图的那几个几乎用不到于是这里只贴二分图的定义

最小点覆盖：理解为点覆盖边，即用最小的点覆盖所有的边。(若一条边的其中一个端点被选用，这条边就被覆盖了)

最大独立集：求一个最大的点集，里面的点不存在任何的边相连。

最小边覆盖：理解为边覆盖点，用最少的边把图中的点全部覆盖。

最小路径覆盖：用最少的路径把图中的所有点覆盖。

题目大意：

一个矩形中，有N个城市’*’，现在这n个城市都要覆盖无线，若放置一个基站，那么它至多可以覆盖相邻的两个城市。
问至少放置多少个基站才能使得所有的城市都覆盖无线？

解题思路：

思前想后，依稀可以认为是一道求二分图的最小路径覆盖问题

要确认是构造有向图，还是构造无向图，那么就需要先根据题意，看看构造二分图时所使用的方式，更适合构造哪一种二分图。

如何构造二分图

首先要明确的是，输入的一堆“圈圈星星”可以看做是一张大地图，地图上有所有城市的坐标，但是这里有一个误区：不能简单地把城市的两个x、y坐标作为准备构造的二分图的两个顶点集。

城市才是要构造的二分图的顶点！

构造方法如下：

例如输入：

*oo

***

O*o

时，可以抽象为一个数字地图：

100

234

050

数字就是根据输入的城市次序作为该城市的编号，0代表该位置没有城市。

然后根据题目的“范围”规则，从第一个城市开始，以自身作为中心城市，向四个方向的城市进行连线（覆盖）

因此就能够得到边集：

e12  e21     e32     e43    e53

     e23     e34

             e35

可以看到，这些边都是有向边，但是每一条边都有与其对应的一条相反边。

即任意两个城市（顶点）之间的边是成对出现的

那么我们就可以确定下来，应该 构造无向二分图（其实无向=双向）

因为若要构造有向的二分图时，需要判断已出现的边，是很麻烦的工作

为了把有向图G构造为无向二分图，这里需要引入一个新名词“拆点”

其实就是把原有向图G的每一个顶点都”拆分（我认为复制更准确）”为2个点，分别属于所要构造的二分图的两个顶点集

例如在刚才的例子中抽出一条有向边e12举例说明：

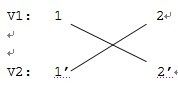
复制顶点1和顶点2，使得1，2∈V1；  1’，2’∈V2 ，不难发现|V1|=|V2|

根据边e12和e21，得到无向二分图：

 

那么同理就可以得到刚才的例子的 无向二分图为：

 

 

无向二分图的最小路径覆盖 = 顶点数 – 最大二分匹配数/2

 

代码：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

int w,h;
char scenario[45][15];
int num[45][15];
int map[410][410];
bool isvisted[410];
int match[410];
int n;

bool path(int u)
{
	for (int i = 1; i <= n; ++ i)
	{
		if (map[u][i] && !isvisted[i])
		{
			isvisted[i] = true;
			if (match[i] == -1 || path(match[i]))
			{
				match[i] = u;
				return true;
			}
		}
	}
	return false;
}
void buildMap()
{
	memset(map, 0, sizeof(map));
	memset(num, 0, sizeof(num));
	n = 0;
	for (int i = 1; i <= h;  ++ i)
	{
		for (int j = 1; j <= w; ++ j)
		{
			if (scenario[i][j] == '*')
			{
				num[i][j] = ++n;
			}
		}
	}
	for (int i = 1; i <= h;  ++ i)
	{
		for (int j = 1; j <= w; ++ j)
		{
			if (num[i][j] > 0)
			{
				if (num[i - 1][j] > 0)
				{
					map[num[i][j]][num[i - 1][j]] = 1;
				}
				if (num[i + 1][j] > 0)
				{
					map[num[i][j]][num[i + 1][j]] = 1;
				}
				if (num[i][j - 1] > 0)
				{
					map[num[i][j]][num[i][j - 1]] = 1;
				}
				if (num[i][j + 1] > 0)
				{
					map[num[i][j]][num[i][j + 1]] = 1;
				}
				//num[i][j] = 0;
			}
		}
	}
}
int main()
{
	int t;
	scanf("%d", &t);
	while (t --)
	{
		int count = 0;
		scanf("%d %d", &h, &w);
		memset(scenario, 0, sizeof(scenario));
		memset(match, -1, sizeof(match));
		for (int i = 1; i <= h; ++ i)
		{
			scanf("%s", &scenario[i][1]);
		}
		buildMap();
		for (int i = 1; i <= n; ++ i )
		{
			memset(isvisted, false, sizeof(isvisted));
			if (path(i))
			{
				++count;
			}
		}
		printf("%d\n", n - count/2);
	}
	return 0;
}