第六周上机实践项目——用多文件组织多个类的程序
/* *程序的版权和版本声明部分: *Copyright(c)2014,烟台大学计算机学院学生 *All rights reserved. *文件名称: *作者:刘中林 *完成日期:2014 年 4 月 1 日 *版本号:v1.0 *对任务及求解方法的描述部分: *输入描述:能构成三角形的三个点坐标 *问题描述: *程序输出:- -周长、面积、是否为直角三角形、是否为等腰三角形 *问题分析:两个类 *算法设计: */
main.cpp:
#include<iostream>
#include<cmath>
#include"shengming.h"
using namespace std;
int main()
{
CPoint x,y,z;
cout<<"请输入三组坐标:"<<endl;
x.input();
y.input();
z.input();
CTriangle t1(x,y,z);
t1.settriangle();
cout<<"三角形的周长:"<<t1.perimeter()<<endl;
cout<<"三角形的面积:"<<t1.area()<<endl;
if(t1.isIsoscelesTriangle())
cout<<"该三角形是等腰三角形"<<endl;
else
cout<<"该三角形不是等腰三角形"<<endl;
if(t1.isRightTriangle())
cout<<"该三角形是直角三角形"<<endl;
else
cout<<"该三角形不是直角三角形"<<endl;
return 0;
}
shengming.h:
#ifndef SHENGMING_H_INCLUDED
#define SHENGMING_H_INCLUDED
class CPoint
{
public:
CPoint(double xx=0,double yy=0):x(xx),y(yy){}
double Distance(CPoint p) const; // 两点之间的距离
void input(); //以x,y 形式输入坐标点
private:
double x; // 横坐标
double y; // 纵坐标
};
class CTriangle
{
public:
CTriangle(CPoint &X,CPoint &Y,CPoint &Z):A(X),B(Y),C(Z){} //给出三点的构造函数
void setTriangle(CPoint &X,CPoint &Y,CPoint &Z);//纽带
void settriangle();//三角形
float perimeter(void);//计算三角形的周长
float area(void);//计算并返回三角形的面积
bool isRightTriangle(); //是否为直角三角形
bool isIsoscelesTriangle(); //是否为等腰三角形
private:
CPoint A,B,C; //三顶点传递
float a,b,c;//三边长
};
#endif // SHENGMING_H_INCLUDED
hanshu.cpp:
#include<iostream>
#include"shengming.h"
#include<Cmath>
using namespace std;
void CPoint::input()
{
cout<<"请输入坐标:";
cin>>x>>y;
}
double CPoint::Distance(CPoint p) const
{
return sqrt(pow(x-p.x,2)+pow(y-p.y,2));
}
hanshu2.cpp:
#include<iostream>
#include"shengming.h"
#include<Cmath>
void CTriangle::setTriangle(CPoint &X,CPoint &Y,CPoint &Z)
{
A=X;B=Y;C=Z;
}
void CTriangle::settriangle()//三边
{
a=B.Distance(C);
b=C.Distance(A);
c=A.Distance(B);
}
float CTriangle::perimeter(void)//计算三角形的周长
{
return a+b+c;
}
float CTriangle::area(void)//计算并返回三角形的面积
{
float s = (a + b + c) / 2;
return sqrt(s * (s - a) * (s - b) * (s - c));
}
bool CTriangle::isRightTriangle()//是否为直角三角形
{
if(a*a+b*b==c*c||b*b+c*c==a*a||a*a+c*c==b*b)
return true;
else
return false;
}
bool CTriangle::isIsoscelesTriangle() //是否为等腰三角形
{
bool flag=false;
if(a==b||a==c||b==c)
flag=true;
return flag;
}
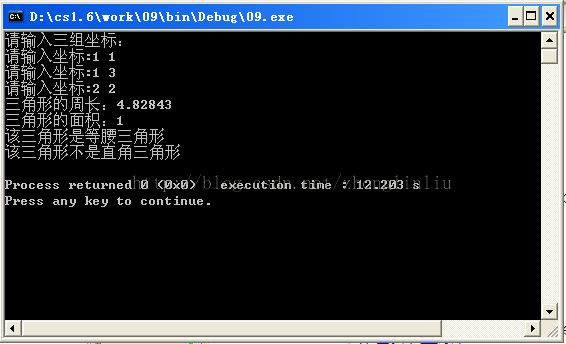
*样例输出:
*心得体会:有些已经冷淡的东西,当我们渐渐的发现还能学到关于它的新东西的时候,便会激情复燃。。