在matlab中做数据拟合是非常常见的事,而又以多项式拟合最为常用,下面简单介绍一下常见的多项式拟合的方法:
多项式拟合
1. 多项式拟合命令
x=[1 2 3 4 5 6 7 8 9]; y=[9 7 6 8 5 2 4 10 30]; %导入拟合的数据P=polyfit(x, y, 3); %多项式拟合,返回降幂排列的多项式系数,这里3是拟合的最高次幂
xi=0:0.2:10; %要求的点的横坐标
yi=polyval(P, xi); %计算多项式的值
plot(xi, yi, x, y, 'r*'); %出图,默认的蓝色线是拟合的曲线,红色*是离散点
2. 图形窗口的多项式拟合
在图形窗口可以用菜单的方式对数据进行简单,高效的拟合,首先画出原始的离散数据点:
y=[9 7 6 8 5 2 4 10 30]; %导入拟合的数据
plot(x,y,'r*')
生成了原始离散图形之后,在图形窗口单击:Tools-->Basic Fitting,打开对话框,可以看到可以使用几种不同的多项式拟合方式,并且可以同时多项勾选,例如同时进行线性、二阶、三阶拟合。下面可以使用各种图形显示残差。
曲线拟合工具箱
下面重点详述matlab提供了曲线拟合工具箱。依次单击Start-->Toolboxes-->Curve Fitting-->Curve Fitting Tool(cftool)就可以打开曲线拟合工具箱,或者在命令窗口中直接输入cftool命令打开。
可以看到5个命令按钮
Data:可输出、查看和平滑数据;
Fitting:可以拟合数据、比较拟合曲线和数据集;
Exclude:可以从拟合曲线中排除特殊的数据点;
Ploting:在选定区间后,单击按钮,可以显示拟合曲线和数据集;
Analysis:可以做内插法、外推法、微积分或积分拟合。
1. 导入数据集
在导入数据之前,数据变量必须已经存在于matlab的工作区间。在导入数据之后,就会在data对话框中进行X和Y的数据设置。
Data对话框包括两个选项卡:Data Sets和Smooth。
Data Sets选项卡:
这里X data和Y data就是用于选择观测数据和选择X的响应数据
Weight用于选择权重,与响应数据相联系的向量,如果没有选择,默认值为1.
需要注意的是这里把向量输入工作区,主要以变量具有相同的维数,无穷大的值和不定值将被忽略。
当选择Data Sets列表框中的数据集时候,单击view按钮,打开view按钮可以以工作表的方式察看数据。
2. 数据的预处理
在曲线拟合工具箱中,数据的预处理主要包括平滑法、排除法和区间排除法。
2.1 平滑数据
在刚才的选项卡中选择smooth选项卡,下面对smooth选项卡简单介绍一下:
Original data set:用于挑选需要拟合的数据集;
Smoothed data set:平滑数据的名称;
Method:用于选择平滑数据的方法,每一个相应数据结果用通过特殊的曲线平滑方法所计算的结果来取代。平滑数据的方法包括:
1. Moving average:用移动平均值进行替换;
2. Lowess:局部加权散点图平滑数据,采用线性最小二乘法和一阶多项式拟合得到的数据进行替换;
3. Loess:和上面的类似,不同的是使用线性最小二乘法和二阶多项式拟合得到的数据进行交换;
4. Savitzky-Golay:采用未加权的线性最小二乘法过滤数据,利用指定阶数的多项式得到的数据进行替换;
5. Span用于进行平滑计算的数据点的数目;
6. Degree:用于Savitzky-Golay方法拟合多项式的阶数。
2.2. 异常排除
显然一大堆的离散数据中很难保证数据都是可以使用的,必须要对数据中的异常值进行排除。
区间排除法是采用一定的区间去排除那些用与系统误差导致偏离正常值的异常值。
在曲线拟合工具箱中选择Exclude按钮,可以打开Exclude对话框。
Exclusion rule name:用于指定分离规则的名称;
Select data set:挑选需要操作的数据集;
Exclude graphically:允许我们使用图形的方式去除异常值,排除个别的点用“X”标记。
Check to exclude point:挑选个别的点进行排除,可以通过在数据表中打钩来选择要排除的数据。
Exclude Sections:用来选定区域排除数据:
其中Exclude X选择预测数据X要排除的数据范围;
Exclude Y选择响应数据Y要排除的数据范围。
2.3 其他数据预处理的方法
其他的预处理方法不便通过曲线拟合工具箱来视线,主要包括两个部分:
(1). 响应数据的转换
响应数据的转换一般包括对数转换和指数转换,用这些转换可以使非线性的模型线性化,便于曲线拟合。变量的转换一般在命令行里面实现,然后把转换后的数据输入曲线拟合工具箱,然后再进行拟合。
(2). 无穷大、不定值在曲线拟合中是可以忽略,如果想把它们从数据集中删除,可以用isinf和isnan置换无穷大和缺失值。
3. 数据拟合
命令行的方式不再赘述,不是本笔记的重点,简明的命令在前面的例子中已有。
在曲线拟合工具箱的对话框中单击fitting按钮打开fitting对话框进行设置,实现曲线拟合。
同时给出了一些常用的拟合类型:
Exponential:指数拟合包括两种形式
Fourier:傅里叶拟合
Gaussian:高斯法
Interpolant:内插法,包括线性插值、最近邻内插值和shapepreserving插值
polynomial多项式,从一次到九次
Rational有理拟合,两个多项式之比,分子和分母都是多项式
Power指数拟合
Smoothing spline平滑样条拟合,默认的平滑参数由拟合的数据集来决定,参数是0产生一个分段的线性多项式你和,参数是1产生一次分段三次多项式拟合
Sum of Sin Function正弦函数的和
Weibull两个参数的weibull分布
Degree of Freedom Adjusted R-Square调整自由度以后的残差的平方,数值越接近1,曲线的拟合效果越好。
Root Mean Square Error根的均方误差
Table of Fits里面的Table options里面的重点两个参数:
SSE=sum of squares due to error误差平方和,越接近0曲线的拟合效果
R-square越接近1,曲线的拟合效果越好
简单示例一下拟合数据hahn1.m,hahn1.m是matlab自带,描述铜的热膨胀与热力学温度的相关性,包括两个向量temp和thermex。
load hahn1 %载入hahn1的数据cftool %打开曲线拟合工具箱
选择4次多项式拟合,简单上个图把: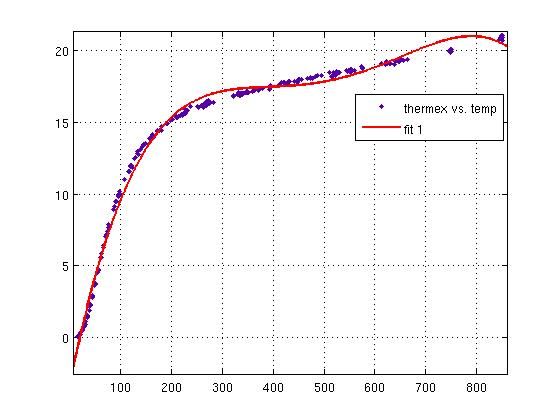
4. 非参数拟合
有时候我们对拟合参数的提取或解释并不感兴趣,只是想得到一个平滑的通过各数据点的曲线,这种拟合曲线的形式就称之为非参数拟合。
非参数拟合的方法包括:
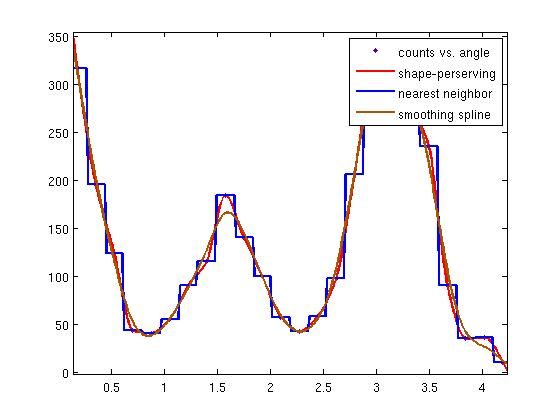
插值法:Interpolants
在已知数据点之间估计数值的过程,包括
Linear线性内差,在每一队数据之间用不同的线性多项式拟合。
Nearest neighbor最近邻内插,内插点在最相邻的数据点之间。
Cubic spline三次样条内插,在每一队数据之间用不同的三次多项式拟合。
Shape-preserving分段三次艾尔米特内插。
平滑样条内插法Smoothing spline
平滑样条内插是对杂乱无章的数据进行平滑处理,可以用平滑数据的方法来拟合,平滑的方法在数据的预处理中已经介绍。
下面使用碳12alpha来进行示例:
load carbon12alphacftool