Exploiting the Circulant Structure of Tracking-by-detection with Kernels 笔记

这是一篇ECCV2014年的paper，在这篇paper中作者提出了kernelized correlation filter，并将其应用到了tracking中，从而有了15年PAMIN的那篇文章，我再之前博客中也记录过

http://blog.csdn.net/carrierlxksuper/article/details/46461245

这篇文章的公式推导比较复杂，感兴趣的可以去看看：http://blog.csdn.net/ikerpeng/article/details/44171159

在这里，我想重新介绍一下KCF，并且加上一点自己的认识。

track-by-detection的方法获得了广泛的应用，这个思想需要首先获取样本进行训练，常用的方法就是 系数采样。如下所示：

这种方法的缺点就是样本之间有重叠，或者叫有冗余并且比较慢，因为一般要采集大量的样本。于是作者想exploite structure.作者的思想就是利用FFT来快速的合并所有subwindows的信息，而不用迭代的采样。

下面开始介绍主要内容。

先说一下作者的motivation: 在tracking-by-detection里面的核心是分类器。训练分类器需要采集正负样本，作者打算采集所有的样本，也就上面图所示的那种dense sampling。

作者首先构造一个model:

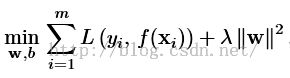------------------------------------------1

这里L是损失函数，x和y分别是训练样本和标签。函数f是： 

如果是线性SVM的话，L的表达式是：，如果是linear regression 的话，L的表达式是：作者指出，很多时候两者效果接近，于是作者用后者代替前者。

那么上面的公式1的闭式解就是：------------------------------2

其中K是核矩阵，我们要求解的是w,这里为什么出来的是\alpha呢。其实这是利用了一个叫表达理论的东西：

，这里有了alpha，就可以获得w了，其中\pha是空间映射函数。为什么要整这么复杂，又是表达理论又是核的，这是因为很多时候没法直接求w必须利用这些技术简化求解。

OK，有了这些理论基础之后，就开始进入下一步了：Circulant matrices。理解这个可以参考我的关于KCF的那篇blog，这里简单介绍一下，就是我们有了一个base sample之后，通过不断的cyclic shift就可以得到一个circulant matrics C(u)，

这个矩阵有什么用呢？就是当我们用它来对vector进行卷积的时候很有用。例如我们表示两个vector u和v的卷积，那么就可固定v不动，让u做cyclic shift得到C(u).那么C(u)v就表示u和v之间的卷积运算。在频率域下就可以表示为：

这些都是为了下面的dense sample做准备。给定一幅图像，假设是vector形式的，那么下面的运算：

每进行一次就相当于对图像采样一次。然后我们利用一个定理：

就可以得到：

然后公式2就变成了：

当新的样本z来了之后，分类器输出为：

上面公式意思是挨个计算xi与输入z之间的卷积运算。如果我们想同时计算z与xi之间的卷积运算，那么 ：

后面就是对K采用的一些核技巧。不再介绍了。