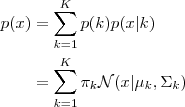高斯混合模型算法

下面介绍一下几种典型的机器算法

首先第一种是高斯混合模型算法:

高斯模型有单高斯模型（SGM）和混合高斯模型（GMM）两种。

（1）单高斯模型：

为简单起见，阈值t的选取一般靠经验值来设定。通常意义下，我们一般取t=0.7-0.75之间。

二维情况如下所示：

（2）混合高斯模型：

 

      对于(b)图所示的情况，很明显，单高斯模型是无法解决的。为了解决这个问题，人们提出了高斯混合模型（GMM），顾名思义，就是数据可以看作是从数个高斯分布中生成出来的。虽然我们可以用不同的分布来随意地构造 XX Mixture Model ，但是 GMM是 最为流行。另外，Mixture Model 本身其实也是可以变得任意复杂的，通过增加 Model 的个数，我们可以任意地逼近任何连续的概率密分布。

    每个 GMM 由 K 个 Gaussian 分布组成，每个 Gaussian 称为一个“Component”，这些 Component 线性加成在一起就组成了 GMM 的概率密度函数：

 

                （1）

其中，πk表示选中这个component部分的概率，我们也称其为加权系数。

根据上面的式子，如果我们要从 GMM 的分布中随机地取一个点的话，实际上可以分为两步：

（1）首先随机地在这 K 个 Component 之中选一个，每个 Component 被选中的概率实际上就是它的系数 πk，选中了 Component 之后，再单独地考虑从这个 Component 的分布中选取一个点就可以了──这里已经回到了普通的 Gaussian 分布，转化为了已知的问题。假设现在有 N 个数据点，我们认为这些数据点由某个GMM模型产生，现在我们要需要确定 πk,μk,σk 这些参数。很自然的，我们想到利用最大似然估计来确定这些参数，GMM的似然函数如下：

        （2）

 

在最大似然估计里面，由于我们的目的是把乘积的形式分解为求和的形式，即在等式的左右两边加上一个log函数，但是由上文博客里的（2）式可以看出，转化为log后，还有log(a+b)的形式，因此，要进一步求解。

我们采用EM算法，分布迭代求解最大值：

EM算法的步骤这里不作详细的介绍，可以参见博客：

http://blog.pluskid.org/?p=39

贴出代码：

  1 function varargout = gmm(X, K_or_centroids)
  2 % ============================================================
  3 % Expectation-Maximization iteration implementation of
  4 % Gaussian Mixture Model.
  5 %
  6 % PX = GMM(X, K_OR_CENTROIDS)
  7 % [PX MODEL] = GMM(X, K_OR_CENTROIDS)
  8 %
  9 %  - X: N-by-D data matrix.
 10 %  - K_OR_CENTROIDS: either K indicating the number of
 11 %       components or a K-by-D matrix indicating the
 12 %       choosing of the initial K centroids.
 13 %
 14 %  - PX: N-by-K matrix indicating the probability of each
 15 %       component generating each point.
 16 %  - MODEL: a structure containing the parameters for a GMM:
 17 %       MODEL.Miu: a K-by-D matrix.
 18 %       MODEL.Sigma: a D-by-D-by-K matrix.
 19 %       MODEL.Pi: a 1-by-K vector.
 20 % ============================================================
 21  
 22     threshold = 1e-15;
 23     [N, D] = size(X);
 24  
 25     if isscalar(K_or_centroids)
 26         K = K_or_centroids;
 27         % randomly pick centroids
 28         rndp = randperm(N);
 29         centroids = X(rndp(1:K), :);
 30     else
 31         K = size(K_or_centroids, 1);
 32         centroids = K_or_centroids;
 33     end
 34  
 35     % initial values
 36     [pMiu pPi pSigma] = init_params();
 37  
 38     Lprev = -inf;
 39     while true
 40         Px = calc_prob();
 41  
 42         % new value for pGamma
 43         pGamma = Px .* repmat(pPi, N, 1);
 44         pGamma = pGamma ./ repmat(sum(pGamma, 2), 1, K);
 45  
 46         % new value for parameters of each Component
 47         Nk = sum(pGamma, 1);
 48         pMiu = diag(1./Nk) * pGamma' * X;
 49         pPi = Nk/N;
 50         for kk = 1:K
 51             Xshift = X-repmat(pMiu(kk, :), N, 1);
 52             pSigma(:, :, kk) = (Xshift' * ...
 53                 (diag(pGamma(:, kk)) * Xshift)) / Nk(kk);
 54         end
 55  
 56         % check for convergence
 57         L = sum(log(Px*pPi'));
 58         if L-Lprev < threshold
 59             break;
 60         end
 61         Lprev = L;
 62     end
 63  
 64     if nargout == 1
 65         varargout = {Px};
 66     else
 67         model = [];
 68         model.Miu = pMiu;
 69         model.Sigma = pSigma;
 70         model.Pi = pPi;
 71         varargout = {Px, model};
 72     end
 73  
 74     function [pMiu pPi pSigma] = init_params()
 75         pMiu = centroids;
 76         pPi = zeros(1, K);
 77         pSigma = zeros(D, D, K);
 78  
 79         % hard assign x to each centroids
 80         distmat = repmat(sum(X.*X, 2), 1, K) + ...
 81             repmat(sum(pMiu.*pMiu, 2)', N, 1) - ...
 82             2*X*pMiu';
 83         [dummy labels] = min(distmat, [], 2);
 84  
 85         for k=1:K
 86             Xk = X(labels == k, :);
 87             pPi(k) = size(Xk, 1)/N;
 88             pSigma(:, :, k) = cov(Xk);
 89         end
 90     end
 91  
 92     function Px = calc_prob()
 93         Px = zeros(N, K);
 94         for k = 1:K
 95             Xshift = X-repmat(pMiu(k, :), N, 1);
 96             inv_pSigma = inv(pSigma(:, :, k));
 97             tmp = sum((Xshift*inv_pSigma) .* Xshift, 2);
 98             coef = (2*pi)^(-D/2) * sqrt(det(inv_pSigma));
 99             Px(:, k) = coef * exp(-0.5*tmp);
100         end
101     end
102 end

    函数返回的 Px 是一个  的矩阵，对于每一个  ，我们只要取该矩阵第  行中最大的那个概率值所对应的那个 Component 为  所属的 cluster 就可以实现一个完整的聚类方法了。

 

参考资料：

【C++代码】

http://www.cppblog.com/Terrile/archive/2011/01/19/120051.html

http://www.autonlab.org/tutorials/gmm.html

http://bubblexc.com/y2011/8/

http://blog.pluskid.org/?p=39&cpage=1#comments