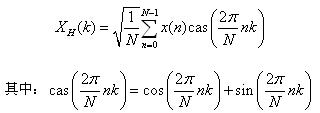压缩感知稀疏基之离散哈特莱变换(DHT)和离散W变换
题目:压缩感知稀疏基之离散哈特莱变换(DHT)和离散W变换
在前面的《压缩感知的常见稀疏基名称及离散傅里叶变换基》中提到了DWT,并没有提到离散哈特莱变换(Discrete Hartley Transform, DHT),但讨论正交变换理论下的稀疏基,比较常见的正交变换应该提一下的,虽然前面提到的DWT也不知道是不是指的离散W变换,因为一般情况下DWT是指的离散小波变换(DiscreteWavelet Transform, DWT),有时也指离散沃尔什变换(Discrete WalshTransform, DWT),不管它是不是指的离散W变换吧,这里都讨论一下吧,之所以把DHT和离散W变换放到一起是因为DHT是离散W变换的四种形式中的第一种形式。下面提到DWT即指离散W变换而不是离散小波变换等其它变换。
注:有时DHT也用来表示离散哈达玛变换(Discrete HadamardTransform DHT)。
一、离散哈特莱变换(Discrete Hartley Transform, DHT)
哈特莱是一个人名,英文为Hartley,有时音译为哈特利或哈特雷,他在1942年提出连续Hartley变换,42年后于1984年,Bracewell提出了离散Hartley变换(DHT)。
在这里,我直接将DHT公式给成正交变换的形式:
上面定义式中我直接将定标因子写为1/N的开方,这样保证DHT的变换矩阵HN直接是正交矩阵:
观察发现矩阵HN不但是正交矩阵并且还是对称矩阵(转置与本身相等),因此逆矩阵与本身相等(正交矩阵的逆矩阵等于其转置),即DHT的逆变换与正变换形式相同。
DHT也有四种形式,上面给出的是第一种形式,其它参见维基百科【1】。
二、离散W变换(Discrete W Transform, DWT)
有关离散W变换,我一直想找出它的全中文名字,但我查了好久也没有找到,英文文献中是以DiscreteW Transform来表述的,中文文献中是以离散W变换来表述的。离散W变换是由王中德提出的,所以我猜这里的“W”应该是指其姓氏“王(Wang)”的首字母W,因此若要找出它的全中文名字应该是“离散王中德变换”,当然提出者也没有这么命名,这里纯属我自己推测了。
采用文献【2】中的定义,离散W变换定义如下:
其中α和β分别是时域和频率的参数,它们的取值可以是(0,0)、(1/2,0)、(0,1/2)、(1/2,1/2)中的任一个,也就是说DWT共有四种形式,依次为DWT-Ⅰ、DWT-Ⅱ、DWT-Ⅲ、DWT-IV。可以发现,当取(0,0)时的DWT-Ⅰ即为DHT(利用和差化积公式将求和里面的sin展开即可)。
DWT-Ⅳ不但可以得到信号整数倍的谐波,而且可以得到分数倍的谐波。
三、离散W变换奠基人王中德介绍
在网上搜索了“王中德”这个人,却搜不到任何有用信息,感觉如此关注于基础研究的人,无论是IEEE还是其它权威期刊上发表过很多文章,网上竟然没有他的信息,无论是正面的还是负面的。在网络如此发达的今天,哪怕是一个博导教授一般在百度百科里也有会的,不知道到底是为什么没有王先生的信息。最终我从两篇论文中找到了一些有关王中德的个人信息,总结如下:
王中德,1937年3月19日生于江苏南京,1960年毕业于云南大学物理系,毕业后在昆明物理所工作,1980年至1983年在美国亚利桑那(Arizona)大学电机系数字图像分析实验室进修,曾获美国国家自然科学基金,后来到北京邮电学院电信工程系工作。研究方向包括算法研究、信号处理、图像处理等。IEEE高级会员、美国数学学会会员、中国电子学会会员、中国物理学会会员。

四、如何得到DHT基和DWT基
(1)离散W变换
其实写一个通用的函数得到四种离散W变换的变换矩阵就已经得到了DHT的变换矩阵,所以这里先讨论DWT。
Matlab中有dwt函数,但并不是指的离散W变换,而是离散小波变换,谁让小波变换更牛更广一些呢,这里我给出一个离散W变换的Matlab函数:
function [ X ] = DWangT( x,dwt_type )
%DWangT Summary of this function goes here
% Detailed explanation goes here
% x is the input single
% dwt_type decides DWangT types
% X is the discrete W transform of x
N = length(x);
[x_rows,x_columns] = size(x);
if x_rows<x_columns
x = x';%x should be a column vector
end
[k,n] = meshgrid(0:N-1);
if dwt_type==2
alpha = 1/2;
beta = 0;
elseif dwt_type==3
alpha = 0;
beta = 1/2;
elseif dwt_type==4
alpha = 1/2;
beta = 1/2;
else
alpha = 0;
beta = 0;
end
WN = sqrt(2/N) * sin(pi/4 + 2*pi/N * (n+alpha) .* (k+beta));
X = WN*x;
end
这里根据输入参数dwt_type的值决定是哪一种离散W变换。
若要得到得到离散W变换的变换矩阵,稍微把上面函数变一下形就可以了:
function [ WN ] = DWangTmtx( N,dwt_type )
%DWangTmtx Summary of this function goes here
% Detailed explanation goes here
% N is the dimension of WN
% dwt_type decides DWangT types
% WN is the Discrete W Transform matrix
[k,n] = meshgrid(0:N-1);
if dwt_type==2
alpha = 1/2;
beta = 0;
elseif dwt_type==3
alpha = 0;
beta = 1/2;
elseif dwt_type==4
alpha = 1/2;
beta = 1/2;
else
alpha = 0;
beta = 0;
end
WN = sqrt(2/N) * sin(pi/4 + 2*pi/N * (n+alpha) .* (k+beta));
end
(2)离散哈特莱变换
其实只要令上面的dwt_type=1即可得到DHT变换和DHT变换矩阵,这是还是单独给出DHT的变换函数:
function [ X ] = DHartleyT( x )
%DHartleyT Summary of this function goes here
% Detailed explanation goes here
% x is the input single
% X is the discrete Hartley transform of x
N = length(x);
[x_rows,x_columns] = size(x);
if x_rows<x_columns
x = x';%x should be a column vector
end
[k,n] = meshgrid(0:N-1);
HN = sqrt(1/N)*(cos(2*pi/N*n.*k)+sin(2*pi/N*n.*k));
X = HN*x;
end
若要得到得到离散哈特莱变换的变换矩阵,稍微把上面函数变一下形就可以了:
function [ HN ] = DHartleyTmtx( N ) %DHartleyT Summary of this function goes here % Detailed explanation goes here % N is the dimension of WN % HN is the Discrete Hartley Transform matrix [k,n] = meshgrid(0:N-1); HN = sqrt(1/N)*(cos(2*pi/N*n.*k)+sin(2*pi/N*n.*k)); end
五、结语
离散W变换就说这么多吧,深层次的理解还没有多少,有新理解的话再发文。
参考文献:
【1】维基百科.离散哈特利转换,http://zh.wikipedia.org/zh-cn/離散哈特利轉換
【2】胡广书.数字信号处理理论、算法与实现(第三版)[M]. 北京:清华大学出版社,2012:351-352.