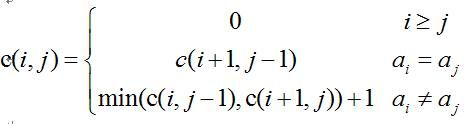POJ1159:Palindrome（回文数）

题目和分析过程来自http://www.java3z.com/cwbwebhome/article/article18/report023.html?id=3947

回文词是一种对称的字符串。任意给定一个字符串，通过插入若干字符，都可以变成回文词。此题的任务是，求出将给定字符串变成回文词所需要插入的最少字符数。 比如 “Ab3bd”插入2个字符后可以变成回文词“dAb3bAd”或“Adb3bdA”，但是插入少于2个的字符无法变成回文词。
[输入] :
第一行:字符串的长度N(3 <= N <= 5000)
第二行:需变成回文词的字符串
[输出] ：
将给定字符串变成回文词所需要插入的最少字符数
[样例] :
Sample Input
5
Ab3bd

Sample Output
2

令c(i,j) 表示将子串aia( i＋1) …aj 变成回文词的最小添加字符数。则这此问题就是要求c(1,n) 。

先来看看求c(1,10)，
一。如果a1＝ a10则c(1,10) ＝c(2,9);
二。如果a1！＝ a10则将a1…a10变成回文词无非只有两种情况：
1.先将 a1…a9变成回文词,再在两头加上a10;
2.先将 a2…a10变成回文词,再在两头加上a1;
即c(1,10) ＝c(1,9)+1或c(1,10) ＝c(2,10)+1.
综合一和二,则变成了求三个c(1,9)，c(2,10)，c(2,9)，如此类推：求c(1,8)，c(2,9)，c(2,8) ；c(2,9)，c(3,10)，c(3,9) ；c(2,8)，c(3,9)，c(3,8).。。。。。

c(i,j)满足如下递推关系：

 

 

代码及其结果如下：

public class POJ1159{ private static int[][] c; private static int n; private static char ss[]; private static void init(){ Scanner sc = new Scanner(System.in); n = sc.nextInt(); ss = sc.next().toCharArray(); c = new int[n][n]; for (int i = 0; i < n; i++) for(int j = 0; j < n; j ++){ c[i][j] = computeMatrixC(i,j); } } private static int getResult(){ return c[0][n - 1]; } /** * c[i,j] = 0(when i >=j) * c[i,j] = c[i + 1, j - 1](when a[i] == a[j]) * c[i,j] = min(c[i,j - 1],c[i + 1,j]) + 1; * @param i * @param j * @return */ private static int computeMatrixC(int i, int j){ if (i >= j) return 0; else if (ss[i] == ss[j]) return computeMatrixC(i + 1, j - 1); else return 1 + (computeMatrixC(i,j - 1) < computeMatrixC(i + 1,j) ? computeMatrixC(i,j - 1): computeMatrixC(i + 1,j)); } public static void main(String[] args){ init(); System.out.println(getResult()); } }

 

5
abcde
4