最长回文子串_POJ3974_O(n)完美求解--------入门级理解

首先你要知道什么是回文串？这个我不解释，然后是让我们求一个字符串的最长回文子串？、

对于如何求解最长回文子串，有几个层次首先当然是暴力求解

其次是找到一个回文串的中心点后向两端扩展，这么做可以求出来但是时间复杂性是O（n）

这一步有一个小亮点就是在对字符串的长度为奇数和偶数的时候采用了统一的处理即先对字符串进行预处理：

在每两个字符之间加入一个特殊字符把原始字符统一变为个数为奇数的新字符，

例如：

121         1#2#1

1221       1#2#2#1

最后一个完美的层次就是对上一步的改进：假设中心点为“i”，r(i)表示回文串的半径，[i-r(i),i]这些为中心点的回文子串的长度是已经求出来的，但是[i+1,i+r(i)]这些的回文子串是未知的，但是我们在求r(i)的时候已经搜索过了因此，就有了改进：（下面为转载）

 

manacher算法:

定义数组p[i]表示以i为中心的(包含i这个字符)回文串半径长

将字符串s从前扫到后for(int i=0;i<strlen(s);++i)来计算p[i],则最大的p[i]就是最长回文串长度,则问题是如何去求p[i]?

由于s是从前扫到后的,所以需要计算p[i]时一定已经计算好了p[1]....p[i-1]

假设现在扫描到了i+k这个位置,现在需要计算p[i+k]

定义maxlen是i+k位置前所有回文串中能延伸到的最右端的位置,即maxlen=p[i]+i;//p[i]+i表示最大的

分两种情况:

1.i+k这个位置不在前面的任何回文串中,即i+k>maxlen,则初始化p[i+k]=1;//本身是回文串

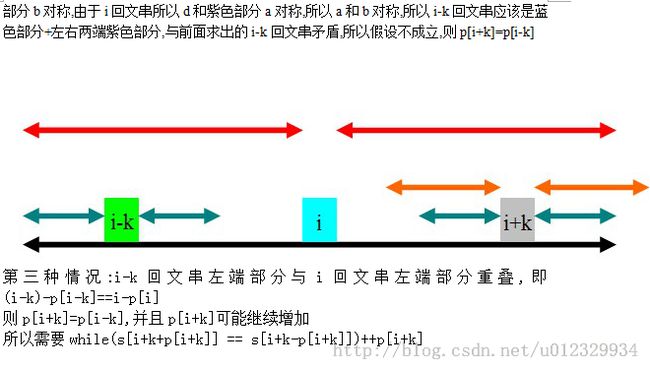
然后p[i+k]左右延伸,即while(s[i+k+p[i+k]] == s[i+k-p[i+k]])++p[i+k]

2.i+k这个位置被前面以位置i为中心的回文串包含,即maxlen>i+k

这样的话p[i+k]就不是从1开始

由于回文串的性质,可知i+k这个位置关于i与i-k对称,

所以p[i+k]分为以下3种情况得出

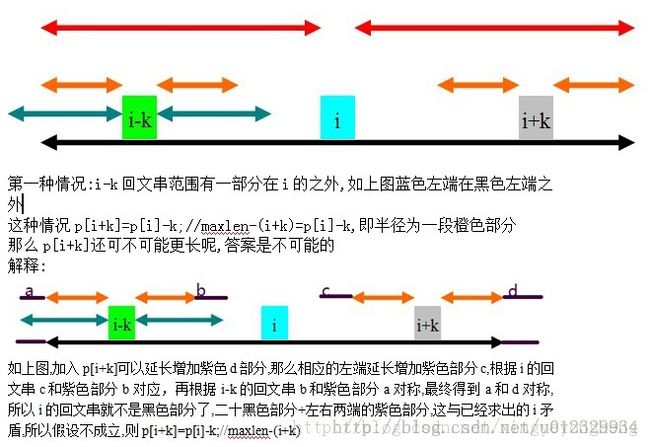
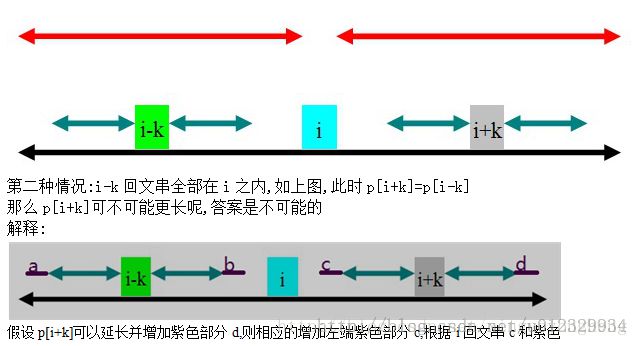
//黑色是i的回文串范围,蓝色是i-k的回文串范围,