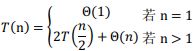《算法导论》读书笔记（三）——分治策略之和最大连续子序列

最大子数组问题

问题描述：

找出一个数组A的和最大非空连续子数组。

一个简单的C++实现：

#include <iostream>

using namespace std;

template <typename T>
T find_Max_Crossing_Subarray(T a[],int low, int high, int mid)
{
	T max_Left = a[mid];
	T max_Right = a[mid + 1];
	T left = a[mid];
	T right = a[mid + 1];
	for(int i = mid - 1; i >= low; i--)
	{
		left += a[i];
		max_Left = max_Left > left ? max_Left : left;
	}
	for(int i = mid + 2; i <= high; i++)
	{
		right += a[i];
		max_Right = max_Right > right ? max_Right : right;
	}
	return max_Left + max_Right;
}

template <typename T>
T find_Max(T a[],int low, int high)
{
	if(high > low)
	{
		int mid = (low + high) / 2;
		T max1 = find_Max(a, low, mid);
		T max2 = find_Max(a, mid + 1, high);
		T max3 = find_Max_Crossing_Subarray(a, low, high, mid);
		T max2or3 = max2 > max3 ? max2 : max3;
		return max1 > max2or3 ? max1 : max2or3;
	}
	else
	{
		return a[low];
	}
}

int main()
{
	int a[15] = {13,-3,-25,20,-3,-16,-23,18,20,-7,12,-5,-22,15,-4};
	cout << find_Max(a, 0, 15) << endl;
	return 0;
}

分治最大子序列算法的递归式：

可以用主方法求得其时间界为O(nlogn)

线性时间界解法

分治法不一定做的最好，最大子序列有线性时间解法，简单的C++实现如下：

#include <iostream>
using namespace std;

template <typename T, int N>
T find_Max(T (&a)[N])
{
	T max = a[0];
	T sum = a[0];
	for(int i = 1; i < N; i++)
	{
		if(sum < 0)
		{
			sum = 0;
		}
		sum += a[i];
		if(max < sum)
		{
			max = sum;
		}
	}
	return max;
}

int main()
{
	int a[16] = {13,-3,-25,20,-3,-16,-23,18,20,-7,12,-5,-22,15,-4,7};
	cout << find_Max(a) << endl;
	return 0;
}