logistic回归简介

logistic回归

一、名词解释：

logistic回归又称罗杰斯蒂克回归分析，或逻辑回归分析。

Logistic回归为概率型非线性回归模型，是研究分类观察结果y与一些影响因素x（单变量，多变量都可以）之间关系的一种多变量的分析方法 。

 

二、与线性回归的关系

logistic回归与多重线性回归实际上有很多相同之处，最大的区别就在于他们的因变量不同，其他的基本都差不多，正是因为如此，这两种回归可以归于同一个家族，即广义线性模型（generalized linear model）。这一家族中的模型形式基本上都差不多，不同的就是因变量不同，如果是连续的，例如身高，体重等，就是多重线性回归，如果是二项分布（是否有病，是否录取等），就是logistic回归，如果是poisson分布，就是poisson回归，如果是负二项分布，就是负二项回归，等等。只要注意区分它们的因变量就可以了。

logistic回归的因变量可以是二分类的，也可以是多分类的，但是二分类的更为常用，也更加容易解释。所以实际中最为常用的就是二分类（发生为1，不发生为0）的logistic回归。

参考文献：http://baike.baidu.com/link?url=SU6w9d1Ug1RikPPNsldfu8643fvTWvhx78ff2DSik9N4SBxwkRFajD7RQPeAx9D87BfYq3-EuxZYD3DpBVQPNa

三、logistic模型

                                                                      

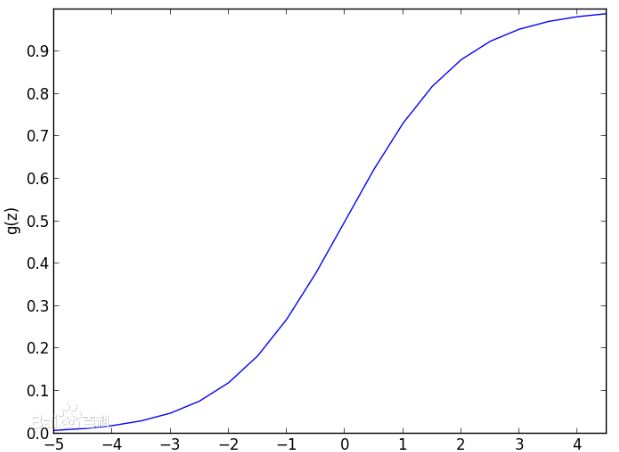
函数图像如下：

                                                                                           

由函数图像可知，

函数的数值特性：值域区间为（0,1），符合概率区间，定义域区间为全体实数R；

函数的形状特性：函数呈现S行的单调递增函数，此函数符合一些生物种群繁殖，人口增长的简单某型。

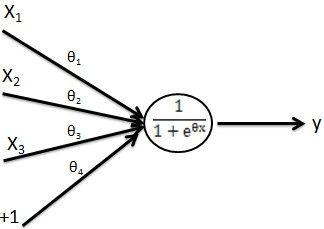
变量x可以为一维变量，也可以为多维变量。类似单变量和多元线性回归。若x为多变量输入，则其数据计算图如下图。

                                

模型函数的详细推导过程详见，线性回归的一种变换：

http://wenku.baidu.com/view/3a1f057602768e9951e73812.html

四、问题描述

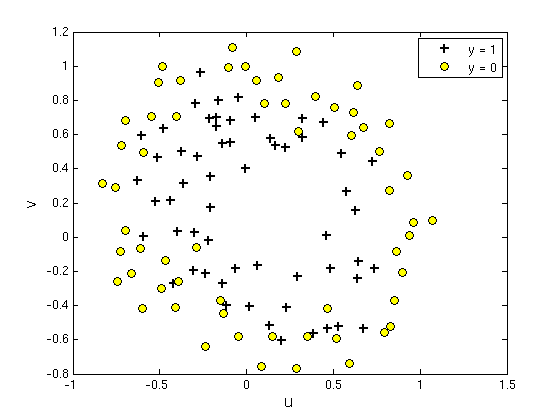
      给出一些学生两门课程的成绩，和他们是否被录取（y=1，录取；y=0,不被录取）；求解拟合函数h(x),来预测某个同学被录取的可能性。

从给出了具有2个特征的一堆训练数据集，从该数据的分布可以看出它们并不是非常线性可分的，因此很有必要用更高阶的特征来模拟（这个不明觉厉）。例如本程序中个就用到了特征值的6次方来求解。

五、Logistic求解

最后优化求解过程中，本例并没有通过梯度下降算法来优化，而是通过牛顿法来优化，牛顿法比梯度下降算法具有收敛快，结果优的特点；但是由于需要求Hessian，需要额外的内存消耗，而且有些问题不能求解H。

       结果分析，lambda=0时，存在过拟合现象，lambda过大=10时，存在低拟合现象。不大不小最好，具体数值大小依据题而定。

模型建立

代码详见：http://www.cnblogs.com/tornadomeet/archive/2013/03/17/2964858.html

解析详见：http://openclassroom.stanford.edu/MainFolder/DocumentPage.php?course=DeepLearning&doc=exercises/ex5/ex5.html