manacher算法 O(n)求最长回文子串

朴素的做法是求出以每个字符为中心的回文串长度，复杂度为，还需要考虑奇数长度和偶数长度。

而manacher算法可以在O(n)时间内求解，奇数长度和偶数长度可以统一处理。根据回文串的对称性，避免了大量不必要的比较。

处理技巧：

①相邻的字符之间插入一个分隔符，串的首尾也要加，以“#”为例，则长度为n的字符串经过处理之后变成2n+1奇数长度的字符串。为防止向两边扩展时越界，可以在首尾处加两个不匹配的特殊字符，末尾为"\0"无需处理，首部加一个"$"符号。

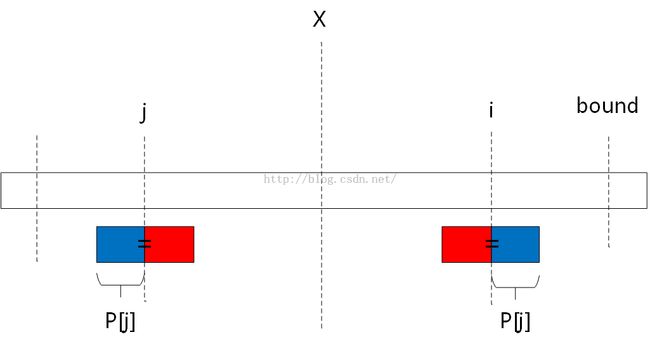
②用一个数组P记录以每个字符为中心的最长回文串半径，假设当前延伸得最远的回文串中心为x，该回文串最远延伸到bound处，此时要求解以i为中心的回文串半径。则：。两种如图所示：

i) i + p[j] <= bound，如下图所示，j的回文串在x的回文串内部，则根据对称性，i处左右p[j]长度的串必定相等，所以i向右p[j]都无需再检查，从p[j]以后开始检查

ii) i + p[j] > bound，如下图所示，j的回文串越过了x的回文串边界，由于以x为中心的最长回文串最多只到bound处，所以bound以后的部位未知，只能跳过bound - i长度的检查。

下面说明p[i]与最长回文串长度的关系。

①中心i为字符时，说明原回文串的长度为奇数（#…#a#…#），则回文串长度为(2 * p[i] - 1 - 1) / 2 = p[i] - 1;

②中心i为'#'时，说明原回文串长度为偶数（#…a#a…#），则回文串长度为(2 * p[i] - 1 - 1) / 2 = p[i] - 1；

例题：http://acm.hdu.edu.cn/showproblem.php?pid=3068，代码如下：

#include <cstdio>
#include <cstring>
using namespace std;
#define N 110005
#define min(a, b) (a) < (b) ? (a) : (b)
char s[N], a[N << 1];
int p[N << 1];

int main(){
    while(scanf("%s", s) == 1){
        getchar();
        int len = strlen(s);
        a[0] = '$';
        int j = 1;
        for(int i = 0; i <= len; ++i){
            a[j] = '#', a[j + 1] = s[i];
            j += 2;
        }
        int n = j, bound = 0, cur, ans = 0;
        for(int i = 1; i < n; ++i){
            if(bound > i)
                p[i] = min(p[cur * 2 - i], bound - i);
            else
                p[i] = 1;
            while(a[i + p[i]] == a[i - p[i]])
                ++p[i];
            if(p[i] + i > bound){
                bound = p[i] + i;
                cur = i;
            }
            if(p[i] > ans)
                ans = p[i];
        }
        printf("%d\n", ans - 1);
        getchar();
    }
    return 0;
}