POJ 1692 Crossed Matchings

 

Crossed Matchings

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 1578		Accepted: 1020

Description

There are two rows of positive integer numbers. We can draw one line segment between any two equal numbers, with values r, if one of them is located in the first row and the other one is located in the second row. We call this line segment an r-matching segment. The following figure shows a 3-matching and a 2-matching segment. 

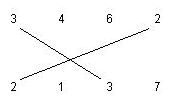
We want to find the maximum number of matching segments possible to draw for the given input, such that: 
1. Each a-matching segment should cross exactly one b-matching segment, where a != b . 
2. No two matching segments can be drawn from a number. For example, the following matchings are not allowed. 

Write a program to compute the maximum number of matching segments for the input data. Note that this number is always even.

Input

The first line of the input is the number M, which is the number of test cases (1 <= M <= 10). Each test case has three lines. The first line contains N1 and N2, the number of integers on the first and the second row respectively. The next line contains N1 integers which are the numbers on the first row. The third line contains N2 integers which are the numbers on the second row. All numbers are positive integers less than 100.

Output

Output should have one separate line for each test case. The maximum number of matching segments for each test case should be written in one separate line.

Sample Input

3
6 6
1 3 1 3 1 3
3 1 3 1 3 1
4 4
1 1 3 3 
1 1 3 3 
12 11
1 2 3 3 2 4 1 5 1 3 5 10
3 1 2 3 2 4 12 1 5 5 3 

Sample Output

6
0
8

Source

Tehran 1999

 

/* 动态规划,类似最长公共子序列,只不过这里面有一个变通,公共子序列变成了两个交叉线 设dp[i][j]表示上界上i到unum,下界从j到dnum可以得到的最大值 则dp子问题分为2个部分 1)从j往dnum扫描到一个位置i',使得up[i] = down[i'],从i网upnum扫描得到一个位置j',使得down[j] = up[j'] 则i i' j j'构成一个公共交叉线,找到所有的这种公共交叉线得到: dp[i][j] = maxv(dp[i’][j‘], 2 + dp[i‘ + 1][j’ + 1] 2)i, j不参与匹配,则有以下三种情况 dp[i][j] = maxv(dp[i][j], dp[i + 1][j], dp[i][j + 1], dp[i + 1][j + 1] 最终结果dp[1][1]即为答案 一开始用递归做的,用时30多毫秒,后来改成自底向上非递归方式也用了30毫秒,看来这个不是优化的关键, 两个版本的程序分别如下: */ //递归方式 #include <iostream> #define maxv(a, b) ((a) >= (b) ? (a) : (b)) #define minv(a, b) ((a) <= (b) ? (a) : (b)) #define MAX_N 100 using namespace std; int up[MAX_N + 1], down[MAX_N + 1]; int unum, dnum; int maxNum; int dp[MAX_N + 1][MAX_N + 1]; int dpsolve(int u, int d) { if(u >= unum || d >= dnum) return 0; if(dp[u][d] != INT_MAX) return dp[u][d]; int maxNum = 0; for(int d1 = d + 1; d1 <= dnum; d1++) { if(up[u] != down[d1]) continue; for(int u1 = u + 1; u1 <= unum; u1++) { if(down[d] != up[u1] || up[u] == up[u1]) continue; maxNum = maxv(maxNum, 2 + dpsolve(u1 + 1, d1 + 1)); } } maxNum = maxv(maxNum, dpsolve(u + 1, d + 1)); maxNum = maxv(maxNum, dpsolve(u + 1, d)); maxNum = maxv(maxNum, dpsolve(u, d + 1)); return dp[u][d] = maxNum; } int main() { int caseNum, i, j; scanf("%d", &caseNum); while(caseNum--) { scanf("%d%d", &unum, &dnum); for(i = 1; i <= unum; i++) scanf("%d", &up[i]); for(i = 1; i <= dnum; i++) scanf("%d", &down[i]); maxNum = INT_MIN; for(i = 1; i <= unum; i++) for(j = 1; j <= dnum; j++) dp[i][j] = INT_MAX; dpsolve(1, 1); printf("%d/n", dp[1][1]); } return 0; } //非递归方式 #include <iostream> #define maxv(a, b) ((a) >= (b) ? (a) : (b)) #define minv(a, b) ((a) <= (b) ? (a) : (b)) #define MAX_N 100 using namespace std; int up[MAX_N + 1], down[MAX_N + 1]; int unum, dnum; int maxNum; int dp[MAX_N + 1][MAX_N + 1]; void dpsolve() { int u, d, uu, dd; for(u = unum; u >= 1; u--) { for(d = dnum; d >= 1; d--) { int maxNum = 0; for(dd = d + 1; dd <= dnum; dd++) { if(up[u] != down[dd]) continue; for(uu = u + 1; uu <= unum; uu++) { if(down[d] != up[uu] || up[u] == up[uu]) continue; if(uu + 1 <= unum && dd + 1 <= dnum )maxNum = maxv(maxNum, 2 + dp[uu + 1][dd + 1]); else maxNum = maxv(maxNum, 2); } } if(d + 1 <= dnum) maxNum = maxv(maxNum, dp[u][d + 1]); if(u + 1 <= unum) maxNum = maxv(maxNum, dp[u + 1][d]); if(d + 1 <= dnum && u + 1 <= unum) maxNum = maxv(maxNum, dp[u + 1][d + 1]); dp[u][d] = maxv(maxNum, dp[u][d]); } } } int main() { int caseNum, i, j; scanf("%d", &caseNum); while(caseNum--) { scanf("%d%d", &unum, &dnum); for(i = 1; i <= unum; i++) scanf("%d", &up[i]); for(i = 1; i <= dnum; i++) scanf("%d", &down[i]); maxNum = INT_MIN; for(i = 1; i <= unum; i++) for(j = 1; j <= dnum; j++) dp[i][j] = 0; dpsolve(); printf("%d/n", dp[1][1]); } return 0; }