寻找最远点对
给定平面上N个点的坐标,找出距离最远的两个点。
分析
类似于“最近点对问题”,这个问题也可以用枚举的方法求解,时间复杂度O(n^2)。
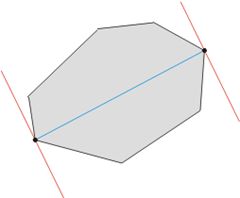
“寻找最近点对”是用到分治策略降低复杂度,而“寻找最远点对”可利用几何性质。注意到:对于平面上有n个点,这一对最远点必然存在于这n个点所构成的一个凸包上(证明略),那么可以排除大量点,如下图所示:
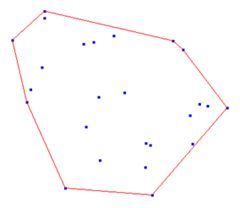
在得到凸包以后,可以只在顶点上面找最远点了。同样,如果不O(n^2)两两枚举,可以想象有两条平行线, “卡”住这个凸包,然后卡紧的情况下旋转一圈,肯定就能找到凸包直径,也就找到了最远的点对。或许这就是为啥叫“旋转卡壳法”。
总结起来,问题解决步骤为:
1、用Graham's Scanning求凸包
2、用Rotating Calipers求凸包直径,也就找到了最远点对。
该算法的平均复杂度为O(nlogn) 。最坏的情况下,如果这n个点本身就构成了一个凸包,时间复杂度为O(n^2)。
下面讲讲Graham's Scanning算法:
凸包:点集Q的凸包(convec hull)是一个最小的凸多边形P,满足Q中的所有点或者在P的边界上,或者在P的内部。
例如:
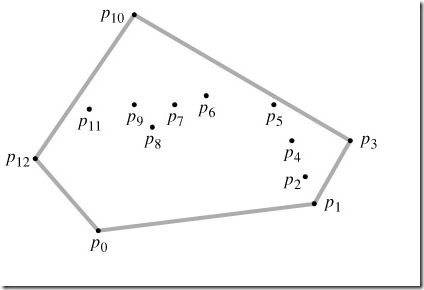
点集Q={p0, p1, …,p12}及其以灰色显示的凸包CH(Q)
这里介绍一种求凸包所包含点集的方法—Graham Scan。
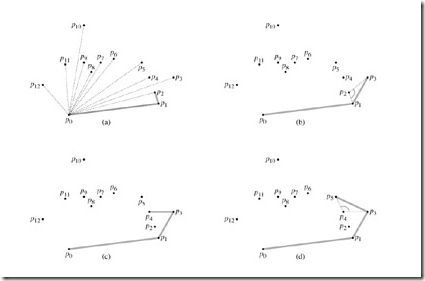
这里在《算法导论》第33章计算几何学的第三节“寻找凸包”讲的很详细,还是以上图为例,看看凸包的建造过程:
步骤1:如图(a),以y轴最低点为基点,找到基点p0。
步骤2:如图(a),以基点p0为一个坐标系的远点,求各点与基点p0的极角,并一次从小到大排序
步骤3:如图(b),按照顺序,每个点都要判断与其前面亮点构成的两条线段转向问题(左转还是右转?用叉积),这个具体看后面伪代码。
步骤4:依次下去,知道所有的点结束,就完成的凸包的寻找。
完整的图见《算法导论》P585~P587页。
这是《算法导论》上的伪代码:
GRAHAM-SCAN(Q) 1 let p0 be the point in Q with the minimum y-coordinate, or the leftmost such point in case of a tie 2 let 〈p1, p2, ..., pm〉 be the remaining points in Q, sorted by polar angle in counterclockwise order around p0 (if more than one point has the same angle, remove all but the one that is farthest from p0) 3 PUSH(p0, S) 4 PUSH(p1, S) 5 PUSH(p2, S) 6 for i ← 3 to m 7 do while the angle formed by points NEXT-TO-TOP(S), TOP(S), and pi makes a nonleft turn 8 do POP(S) 9 PUSH(pi, S) 10 return S
下面讲讲Rotating Calipers算法:
旋转卡壳可以用于求凸包的直径、宽度,两个不相交凸包间的最大距离和最小距离等。虽然算法的思想不难理解,但是实现起来真的很容易让人“卡壳”。
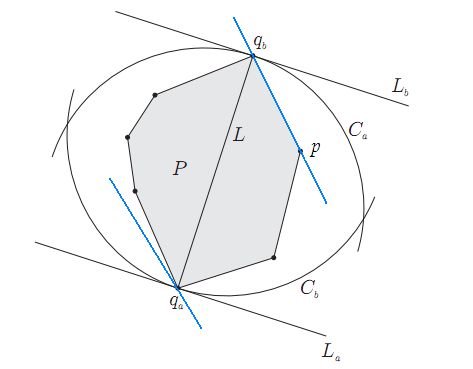
逆向思考,如果qa,qb是凸包上最远两点,必然可以分别过qa,qb画出一对平行线。通过旋转这对平行线,我们可以让它和凸包上的一条边重合,如图中蓝色直线,可以注意到,qa是凸包上离p和qb所在直线最远的点。于是我们的思路就是枚举凸包上的所有边,对每一条边找出凸包上离该边最远的顶点,计算这个顶点到该边两个端点的距离,并记录最大的值。直观上这是一个O(n2)的算法,和直接枚举任意两个顶点一样了。但是注意到当我们逆时针枚举边的时候,最远点的变化也是逆时针的,这样就可以不用从头计算最远点,而可以紧接着上一次的最远点继续计算,于是我们得到了O(n)的算法。
// 求最远点对
#include<iostream>
#include<algorithm>
using namespace std;
struct point
{
int x , y;
}p[50005];
int top , stack[50005]; // 凸包的点存在于stack[]中
inline double dis(const point &a , const point &b)
{
return (a.x - b.x)*(a.x - b.x)+(a.y - b.y)*(a.y - b.y);
}
inline int max(int a , int b)
{
return a > b ? a : b;
}
inline int xmult(const point &p1 , const point &p2 , const point &p0)
{ //计算叉乘--线段旋转方向和对应的四边形的面积--返回(p1-p0)*(p2-p0)叉积
//if叉积为正--p0p1在p0p2的顺时针方向; if(x==0)共线
return (p1.x-p0.x)*(p2.y-p0.y) - (p1.y-p0.y)*(p2.x-p0.x);
}
int cmp(const void * a , const void * b) //逆时针排序 返回正数要交换
{
struct point *p1 = (struct point *)a;
struct point *p2 = (struct point *)b;
int ans = xmult(*p1 , *p2 , p[0]); //向量叉乘
if(ans < 0) //p0p1线段在p0p2线段的上方,需要交换
return 1;
else if(ans == 0 && ( (*p1).x >= (*p2).x)) //斜率相等时,距离近的点在先
return 1;
else
return -1;
}
void graham(int n) //形成凸包
{
qsort(p+1 , n-1 , sizeof(point) , cmp);
int i;
stack[0] = 0 , stack[1] = 1,stack[2]=2;
top = 2;
for(i = 3 ; i < n ; ++i)
{
while(top > 0 && xmult( p[stack[top]] , p[i] , p[stack[top-1]]) <= 0)
top--; //顺时针方向--删除栈顶元素
stack[++top] = i; //新元素入栈
}
}
int rotating_calipers() //卡壳
{
int i , q=1;
int ans = 0;
stack[top]=0;
for(i = 0 ; i < top ; i++)
{
while( xmult( p[stack[i+1]] , p[stack[q+1]] , p[stack[i]] ) > xmult( p[stack[i+1]] , p[stack[q]] , p[stack[i]] ) )
q = (q+1)%(top);
ans = max(ans , max( dis(p[stack[i]] , p[stack[q]]) , dis(p[stack[i+1]] , p[stack[q+1]])));
}
return ans;
}
int main(void)
{
int i , n , leftdown;
while(scanf("%d",&n) != EOF)
{
leftdown = 0;
for(i = 0 ; i < n ; ++i)
{
scanf("%d %d",&p[i].x,&p[i].y);
if(p[i].y < p[leftdown].y || (p[i].y == p[leftdown].y && p[i].x < p[leftdown].x)) //找到最左下角的点
leftdown = i;
}
swap(p[0] , p[leftdown]);
graham(n);
printf("%d\n",rotating_calipers());
}
return 0;
}
参考资料: