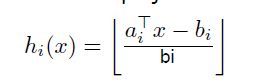BOW模型在ANN框架下的解释

         Bag of words模型（简称BOW）是最常用的特征描述的方法了。在图像分类和检索的相关问题中，能够将一系列数目不定的局部特征聚合为一个固定长度的特征矢量，从而使不同图像之间能够进行直接比较。BOW的改进方法包括一些稀疏的编码方式（如llc）,kernel codebooks等，使得BOW一般作为benchmark被比较。然而，BOW往往作为一种编码方式被解释着（SIFT作为coding，BOW作为average pooling），在这里，我会从一个近似最近邻（approximate nearest neighbor）的角度解释一下BOW。

        假设有两幅图像A和B，A有一系列描述子（例如SIFT）{x1，x2…xn}组成，而B由{y1,y2…ym}组成。为了计算这两幅图之间的相似度，最直接的方法是采用一下的voting system：

   （1）

        其中f是一个匹配函数，反映了xi与yj之间是否匹配。对于一个ε-search和k-NN的匹配方式下，f分别定义为：

 

       按（1）式将所有的i和j累加起来，再对{x}和{y}做归一化（这对应于BOW的L1归一化），就能够得到A和B的一个相似度度量（此时s的值越大，表示A和B之间匹配的特征对的数目越多）。

       我们令f反映的匹配方式为最近邻匹配，此时yj是xi的最近邻时（一般还需要这个最近邻的距离与次近邻的距离的比值小于一定阈值），认为yj和xi是匹配的。但是潜在的一个问题就是如果两幅图包含的SIFT特征十分多（一般是1000以上的数量级），exhaustively search将是十分耗时的，时间复杂度是O(nm)，需要大量的搜索时间。因此常常用approximate nearest neighbor代替exact nearest neighbor，如下图所示。

       近似的最近邻有可能与真实的最近邻有所偏差，但是计算上时间复杂度大大降低。

       常见的ANN的方法有k-d tree（通过生成一棵树对D维特征空间进行划分，待匹配的特征点会从与之属于同一子空间的点开始查找），BBF（改进的k-d tree方法，在k-d tree回溯的时候引入优先级的队列），Locality-sensitive Hashing（通过一系列随机的哈希函数，使得经过哈希投影后两特征点哈希值相等的概率与原特征的相似度之间形成一对应关系）。

   

        LSH是最需要一说的，但是限于篇幅我又不想在这里说，我在后面的文章中肯定会再提到，如果大家不太了解的话可以先看这里。在这里到提到的结论是，对于欧式距离作为相似度的情况下，LSH选择的哈希函数是一个随机的投影函数：

   (2)

        这个投影函数相当于将原始特征向量投影到一条随机的直线上，然后将这条直线划分为长度为bi的多条线段，会落入同一线段上的两特征点被认为是相似的。我们选择多个投影函数共同作用，要求在这多个投影函数上的取值都相等的两个点，才被认为是近邻的。这些投影函数的作用，相当于对整个描述子的特征空间做随机的划分，如下图所示：

        落入同一子空间的点，都被认为是近邻的。至于为什么是随机投影函数，这里有比较详细的解释，我以后有空再到文章中做介绍。

        从LSH的效果上来看，很明显就是我们只要能够选择一种合理的划分特征空间的方式，就能认为落入同一子空间的所有点是近邻的。随机投影尽管能够满足LSH的基本假设，但是这个“随机”，其实是很蛋疼的，因为随着投影的直线越来越多，很多直线存在的意义是值得思考的，也就是说如果我们已经选了1000中随机投影的方法，那么第1001中投影的方法应该尽可能在效果上不同于前1000中（这样才能体现它最大的价值嘛），而随机显然不能保证这一效果。所以，我们完全可以通过所有样本的分布情况，学习出一种划分方式。没错，k-means，无疑是一种实现手段，如下图：

        好，终于绕了半天以后绕到BOW上来了，BOW不就是用k-means训练了一个码数，然后所有SIFT描述子都往这本码数上做硬投影（其实就是投影到一个子空间中）了么。投影后，在同一个码字上的所有点都认为是相匹配的。回到（1）式的f（xi,yj）函数中来，如果xi和yj落入同一个码字上，那么它们就被认为是相匹配的（注意这里一个xi可能与B图像的多个特征相匹配了，我最后还会接着解释）。这种设计，会是f的一种取法。

        再看看BOW的矢量本身，如果我们采用内积来计算两个图像之间的相似度（在此不考虑对BOW矢量做归一化）。BOW特征的第i维表示图像所有SIFT在第i个码字上的投影的数目（对A和B两幅图分别用Ai和Bi表示），那么这一维上内积的结果就是Ai*Bi。这不正是在第i个子空间，A图的所有SIFT点与B图所有SIFT点的两两匹配的所有种可能吗？正好对应着前面所说的f()。

        原来内积对应着两两匹配的所有可能，但是这很不合理啊，一个特征点按理应该在另一幅图中最多找到1个对应的匹配才对，如果用内积来描述相似度，一个点不就被匹配了n多次了么？不合理啊不合理。而如果用直方图相交的话，取min(Ai,Bi)，这样一个点不就最多找到1个对应的匹配了吗？正是因为这样，直方图相交是一种更好的度量BOW这类直方图的方式（而不应该用余弦夹角或者内积）。而从数学上来说，适合L1归一化的特征（直方图一类的特征）不适合用欧氏距离来度量距离，而更适合用Hellinger kernel，Mercer kernel之类的，不过我在这里也不做解释了，大家应该从其他文献中能找到答案。

--------

作者：jiang1st2010

转载请注明出处：http://blog.csdn.net/jwh_bupt/article/details/17540561

http://jiangwh.weebly.com/