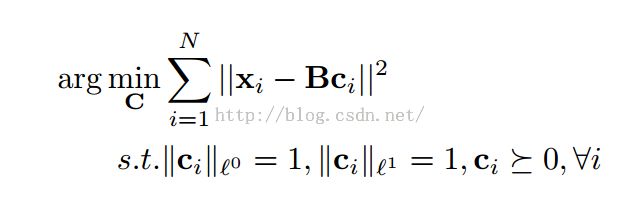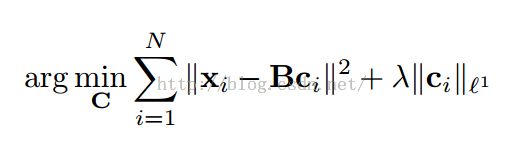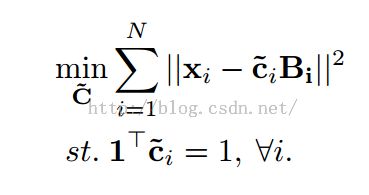Locality-constrained Linear Coding for Image Classification（阅读）

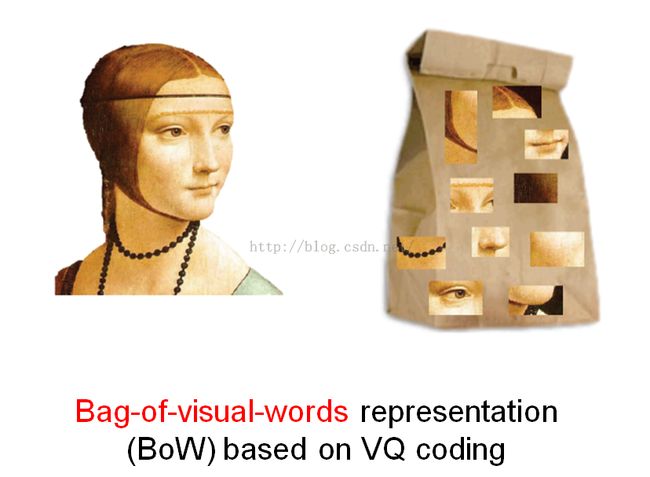
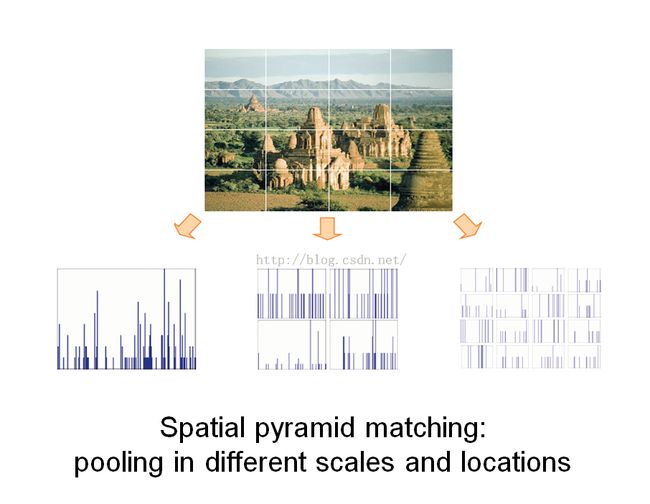
通熟易懂的图片，来自余凯。

经过前面的BoW、BoF、SPM、ScSPM的学习，终于可以大概把CNN网络的结构又有新的理解了：

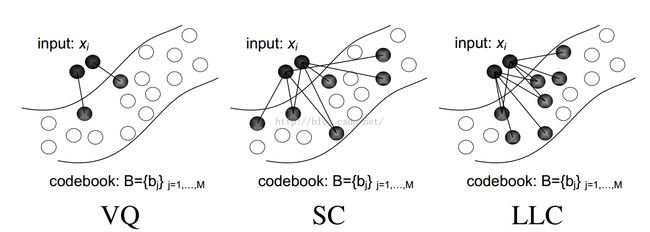
VQ啊，SC啊相当于CNN中的coding部分，SPM相当于pooling部分。

   

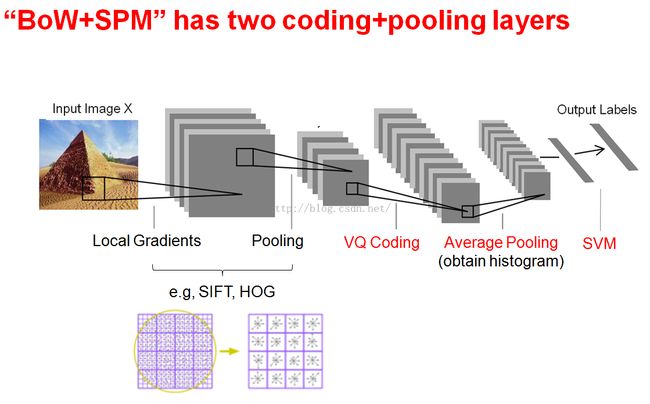
BoW＋SPM的图

下面是CNN等效对比图：

然后接下来就是Spare Coding取代，它能很好模拟人大脑的信号处理过程，求解问题也能够用LASSO解决。

转入正文要说的，这篇论文还是基于SC的进一步修改称为“LLC”。

对比一下每个版本的改进之处：

（X为待编码的特征集，B为codebook，得到的系数向量c为特征对应的编码）

VQ：

SC：

     

LLC：

顺便看一下优化过程的伪代码：

也就是LLC在SC的基础上继续进行的进一步优化，既继承稀疏编码的较小的重构误差性（如前篇文中介绍的），也加入了所谓的局部限制。d中的σ作用是对于局部适应，调整局部的衰减速度，然后1Tci= 1是为了满足sift的LLC要求。d的计算有点像之前高斯权重值，应该就是正态分布对应的值(相邻像素随着距离原始像素越来越远，其权重也越来越小)，保证距离越近权值越高，这样系数矢量中的较大值主要分布在离信号很接近的基上。达到了局部这个意思吧。

这个正则项是2范数，具有局部光滑稀疏的特性。0范数很难优化求解（NP难问题），1范数是0范数的最优凸近似，而且它比0范数要容易优化求解，1范数称Lasso，2范数称Ridge。1范数像一个折线，而2范数这是对折点的曲线化，达到光滑效果，再加上前面的局部化能力和2范数有较好的泛化能力。

再看看这篇文章的分析解部分，有快速的效果，这样设计使得计算复杂度降低了很多。

         

因为由原来的M平方降为（M+K平方），K是很小的，是K-NN的K。

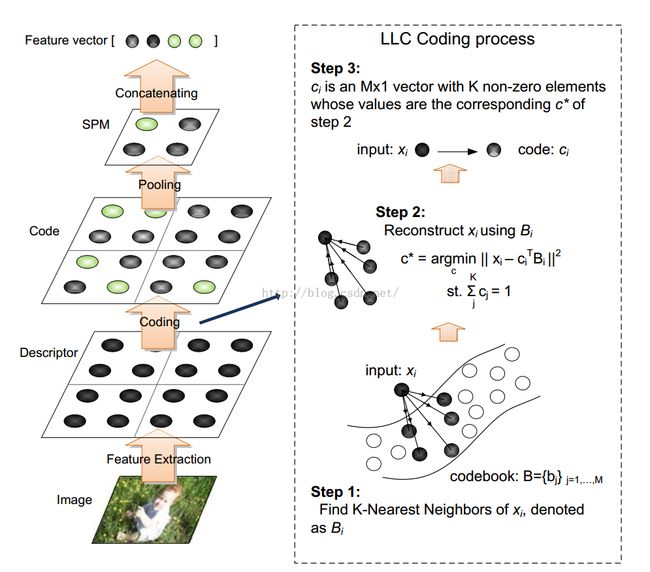
coding过程其实是LLE (Locally Linear Embedding) 局部线性嵌入算法(链接)的前两步

 （1）寻找每个样本点的k个近邻点

% find k nearest neighbors
%       B       -M x d codebook, M entries in a d-dim space
%       X       -N x d matrix, N data points in a d-dim space
XX = sum(X.*X, 2);
BB = sum(B.*B, 2);
D  = repmat(XX, 1, nbase)-2*X*B'+repmat(BB', nframe, 1);
IDX = zeros(nframe, knn);
%(1)寻找每个样本点的k个近邻点
for i = 1:nframe,
	d = D(i,:);
	[dummy, idx] = sort(d, 'ascend');
	IDX(i, :) = idx(1:knn);
end

只需要K近邻，而不需要具体的距离值，而开平方是严格单调函数，保序，因此我们可以省去开平方，节省了计算量。反向索引sort给矩阵每列排序，并返回置换前后下标的映射关系index：index(i,j)是distance第j列第i小的元素的下标。我们要每列前K小的下标，也就是每个Xi的K近邻。任意两个点至少做一次内积O(D)，共O(N^2)个点对，故复杂度：O(DN^2)。

（2）由每个样本点的近邻点计算出该样本点的局部重建权值矩阵

<span style="font-size:18px;">II = eye(knn, knn);
Coeff = zeros(nframe, nbase);
for i=1:nframe
   idx = IDX(i,:);
   z = B(idx,:) - repmat(X(i,:), knn, 1);           % shift ith pt to origin
   C = z*z';      % local covariance
   C = C + II*beta*trace(C);                        % regularlization (K>D)或脊回归，矩阵的对角线加上较小的数，防止C为奇异矩阵
   w = C\ones(knn,1);
   w = w/sum(w);                                    % enforce sum(w)=1
   Coeff(i,idx) = w';
end</span>

这一步用拉格朗日乘数法求此条件极值，从而求得最优解。其他部分的代码应该没有大的修改了。

====================================================================

选择过程的对比

====================================================================

看到论文的大体轮廓然后剖析一下这个idea的支持理论：

Local Coordinate Coding（LCC）来自这篇论文《Nonlinear learning using local coordinate coding》，表示数学功底不够木有看懂，然后参考余凯的PPT，大体理解一下。

这个图应该是基于LCC的局部线性函数改写。

这张是具有局部信息的非线性近似误差函数的连接coding。

正是《Nonlinear learning using local coordinate coding》中的数学理论支撑着LLC。

  余凯认为一个好的编码算法应该满足：

           -   havea small coding error  

           -   and also be sufficiently local

LocalCoordinate Coding学习步骤：

====================================================================