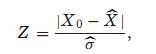随机交换检验数据挖掘结果-assessing data mining result via swap randomization

 

 

这是一篇我比较推崇的文章.06年获得KDD的best paper runner up。近年来数据挖掘在理论上突破很少，这可以算一篇。长久以来，数据挖掘一直关注方法，很少有研究数据集潜在本质的，如何从数据集表现形式去挖掘数据之间更深刻的联系，这篇论文最大亮点就是提出了一种度量数据挖掘方法（尤其是无监督的的方法）在数据集上效果的新思路。

   这篇文章随机交换的思想非常简单，除了第四章有难度，其他章节都十分容易看懂。另外此文书写和内容组织也非常值得借鉴。这篇文章我争取翻译出精华部分，第四章论证部分本人看不懂没法做..第五章是实验我也就懒得翻了；本人翻译水平实在不好，在此还是推荐大家直接阅读原文！

 

 

介绍

数据挖掘中一个重要的研究议题是确定发现的模式或模型是否显著。虽然传统统计方法已经早已用以进行显著性检验，但是在数据挖掘领域这一方法却没有得到足够的重视。在本文中提出采用随机交换来检验在0-1数据集上的数据挖掘结果。随机交换的基本思想是：给定一个数据集D，随机生成一批行间距（row margin）以及列间距(column margin)相同的数据集。在这些随机数据集上进行挖掘，看挖掘结果是否显著不同于在原数据集上的挖掘结果。如果不是，我们可以假设挖掘结果只是由于行间距及列间距的原因，而不是数据集中的有趣结构。

产生这样的数据集是通过交换完成的：对两行u,v和两列,A,B满足uA=vB=1和uB=vA=0，改变行使得uB=vA=1和uA=vB=0.如图所示

 

 

                              

 

 

 

 

 

 

为何要保持行间距列间距一致

    用一个简单的例子说明，给定两个0-1数据集D₁和D₂如图2.5。若使用chi、皮尔逊相关系数考察两个数据集中项X与项Y的相关性会得到相同的结果。这是由于这些相关性检验方法的只考虑到项X和项Y的列(column)属性，因此所有的相关性检验的结果都一致。然而我们看到在D₁中项X与项Y共同出现在差异较大的行(row)里，而在D₂中项X与项Y出现在元素密集的行里，那么我们会猜测D₂中的X与Y的关系并不是由于本身存在有趣的联系，而仅仅是因为它们同时出现在项比较密集的行中。

 

 

                          

                   两个0-1数据集A B，项X与项Y的联系可能是由于整个数据集的作用

 

 

假设项X与项Y是两种超市购物篮数据中的商品，X与Y在D₂数据集表现出的联系是由于许多客户买了几乎所有的商品，而非X与Y商品即存在的内在关联。为了验证假设，文献分别构造了拥有10倍D₁和D₂行数的数据集A，B，显然项X与项Y共现的次数都是60。然后分别生成了1000个随机数据集，在A的随机数据集中，项X与项Y共同次数最大和平均分别为59和52.4；而B的随机数据集中，这两个值分别是69和63.2。那么可以肯定：项X与项Y在A中共现次数更多、项X与项Y的关系存在隐含的联系；而B中项X与项Y的联系少于预期，它们之间的联系可能被高估了。

    行列间距列间距往往隐含了很多数据集上的潜在熟悉，例如在一个以布尔向量表示的文本数据集：行表示文本，列表示词；0代表一个词不在一个文本里出现，1代表出现；行间距代表一个文本里存在的不同的词，列间距代表一个词在文集里使用程度。又度量复杂网络特性的度分布边分布等。因此随机数据集保证行间距列间距固定可以看出数据之间的联系是否只由行列间距决定。

 

 

 

 

 

方法的概述

使D表示一个含有m行n列的0-1数据集，行代表样本，列代表项，0和1分别表示项是否出现在样本中。

我们希望检验一个数据挖掘算法A在D上的结果，令A(D)表示这一结果，为了简单期间，A(D)可以是一个数值，比如频繁模式挖掘中频繁集数量、聚类任务中的聚类错误等等。

在随机交换过程中，产生k个数据集D1, D2…Dk，每个Dt,t=1,2…k也是含m行n列的0-1数据集，算法A在每个数据集上的结果为Xt=A(Dt)，算法显著性可以通过比较A(D)和X={X1,X2…Xk}。

许多方法可以用来检验A(D)显著性。比如p-value

 

 

                       

或Z-score

 

                 

 

 

 

 

 

随机交换的局限

我们相信比较原数据集与随机交换的数据集是一种不错的检验数据挖掘算法的方法。然而何为“有趣”模式并没有统一明确的定义、并且也相当主观，因此不能指望随机交换可以检验出所有的“有趣”模式是否真如此。实际上随机交换的也很明确：检验发现的模式“有趣性”是否直接又行列分布所影响。其他“有趣性”并不被这种方法所包含。另外随机交换只能在二元数据集上进行，而数值属性的数据集上并不适用，另外也不清楚如何对类别属性如何进行随机交换。

 

 

 

 

算法

 

 

朴素的方法(algorimth 1)：

每次在图中找到一对可交换的边(algorithm 2)，进行交换

 

输入：图GD,随机交换步数k

输出：具有行列间距一致的新图GD

第三行用到了算法2

 

 

 

 

 

朴素的方法并不能产生均匀分布的抽样，要达到这点可以采用self loop或Metropolis-Hastings方法

 

 

Self loop方法：

 

 

 

 

 Metropolis-Hastings方法：

 

 

可以看到Self loop方法只是在每次寻找可交换的边时也进行了k的统计，

Metropolis-Hastings方法是在每次找到可交换边后，以 min{1,d(G)/d(G')}概率进行交换。

在实际中self_loop更简单也更快速，Metropolis-Hastings需要计算d(G)/d(G')

 

 

 

关于算法证明和实验大家还是自己看原文比较好，

 

 

 

 

 

 

 

 

翻译得不好请勿见怪~