Bresenham画线算法详解及其OpenGL编程实现

http://blog.csdn.net/xiajun07061225/article/details/7018719

 

Bresenham是由Bresenham提出的一种精确而有效地光栅线生成算法，该算法仅使用增量整数计算。另外，它还可以用于显示其它曲线。

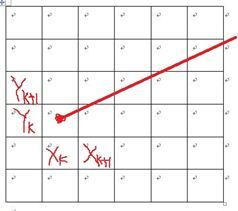
我们以斜率大于0小于1的线段来进行考虑。以单位x间隔进行取样。每次绘制了当前像素点(x_k,y_k)之后，需要确定下一个要绘制的点是(x_k+1,y_k)还是(x_k+1,y_k+1)，需要判断哪一个点像素点更接近线路径。

在取样位置，我们使用d1和d2来表示两个像素和线路径的偏移。在像素列位置x_k+1处的直线上的y坐标可计算为：

y=m(x_k+1)+b

那么：

d1=y-y_k=m(x_k+1)+b-y_k

d2=(y_k+1)-y=y_k+1-m(x_k+1)-b

要确定那个像素点更接近于线路径，需测试这两个像素的偏移的差：

d1-d2=2m(x_k+1)-2y_k+2b-1

为了使用整数进行计算，将决策参数定义为：

p_k=dx*(d1-d2)=2dy*x_k-2dx*y_k+c

pk和d1-d2符号相同。其中m=dy/dx，c=2dy+dx(2b-1)。C是常量，与像素位置无关且会在循环计算pk时被消除。假如y_k处的像素比y_k+1处的像素更接近于线路径，则pk为负，绘制下面的像素。反之为正，绘制上面的像素。

我们可以利用递增整数运算得到后继的决策参数值。由k的式子可以得出：

p_k+1=2dy*x_k+1-2dx*y_k+1+c

则：

p_k+1-p_k=2dy(x_k+1-x_k)-2dx(y_k+1-y_k)

p_k+1=p_k+2dy-2dx(y_k+1-y_k)

而y_k+1-y_k取1或者0取决于p_k的符号。

而起始像素位置(x₀,y₀)的参数p₀可以计算得出：

p₀=2dy-dx

 

由此可以得出斜率大于0小于1的Bresenham画线算法步骤如下：

1、输入线段两个端点坐标，将左端点存储在(x0,y0)中；

2、画出第一个点。

3、计算常量dx,dy,2dy,2dy-2dx。得出第一个决策参数：
p₀=2dy-dx

4、k=0开始，在沿线路径的每个x_k处，进行如下计算：

若p_k<0，下一个要绘制的点是(x_k+1,y_k),且

p_k+1=p_k+2dy。

5、重复步骤4.

编程实现（需要配置OpenGL环境）：

//Bresenham划线算法
//绘制斜率大于0且小于1的线段
#include <GL/glut.h>
#include <iostream>
#include <cmath>
using namespace std;

void init()
{
    glClearColor(1.0,1.0,1.0,1.0);
    glMatrixMode(GL_PROJECTION);
    glLoadIdentity();
    gluOrtho2D(0.0,200.0,0.0,150.0);
}

void display()
{
    int x1 = 10,y1 = 10,x2 = 150,y2 = 100;
    //cout<<"please enter the positions of start point and the end point:x1,y1,x2,y2:"<<endl;
    //cin>>x1>>y1>>x2>>y2;
    int dx = abs(x2 - x1);
    int dy = abs(y2 - y1);
    int x,y;
    int temp1 = 2 * dy;
    int temp2 = 2 * (dy - dx);
    int p = temp1 - dx;
    if(x1 > x2)
    {
        x = x2;
        y = y2;
        x2 = x1;
    }
    else{
        x = x1;
        y = y1;
    }

    glClear(GL_COLOR_BUFFER_BIT);
    glColor3f(1.0,0.0,0.0);
    glBegin(GL_LINES);
        glVertex2i(x,y);
        while(x < x2)
        {
            x++;
            if(p < 0)
                p += temp1;
            else
            {
                y++;
                p += temp2;
            }
            glVertex2i(x,y);
        }
    glEnd();
    glFlush();
}

int main(int argc,char** argv)
{
    glutInit(&argc,argv);
    glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
    glutInitWindowPosition(50,100);
    glutInitWindowSize(400,300);
    glutCreateWindow("Bresenham Draw Line");
    init();
    glutDisplayFunc(display);
    glutMainLoop();
    return 0;
}

//Bresenham划线算法
//绘制斜率大于0且小于1的线段
#include <GL/glut.h>
#include <iostream>
#include <cmath>
using namespace std;

void init()
{
	glClearColor(1.0,1.0,1.0,1.0);
	glMatrixMode(GL_PROJECTION);
	glLoadIdentity();
	gluOrtho2D(0.0,200.0,0.0,150.0);
}

void display()
{
	int x1 = 10,y1 = 10,x2 = 150,y2 = 100;
	//cout<<"please enter the positions of start point and the end point:x1,y1,x2,y2:"<<endl;
	//cin>>x1>>y1>>x2>>y2;
	int dx = abs(x2 - x1);
	int dy = abs(y2 - y1);
	int x,y;
	int temp1 = 2 * dy;
	int temp2 = 2 * (dy - dx);
	int p = temp1 - dx;
	if(x1 > x2)
	{
		x = x2;
		y = y2;
		x2 = x1;
	}
	else{
		x = x1;
		y = y1;
	}

	glClear(GL_COLOR_BUFFER_BIT);
	glColor3f(1.0,0.0,0.0);
	glBegin(GL_LINES);
		glVertex2i(x,y);
		while(x < x2)
		{
			x++;
			if(p < 0)
				p += temp1;
			else
			{
				y++;
				p += temp2;
			}
			glVertex2i(x,y);
		}
	glEnd();
	glFlush();
}

int main(int argc,char** argv)
{
	glutInit(&argc,argv);
	glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
	glutInitWindowPosition(50,100);
	glutInitWindowSize(400,300);
	glutCreateWindow("Bresenham Draw Line");
	init();
	glutDisplayFunc(display);
	glutMainLoop();
	return 0;
}

运行结果：

如有问题，欢迎大家批评指正！