叩开3D编程这扇门

叩开3D编程这扇门  

EmilMatthew([email protected])

摘要: 

       通过透视投影方式，实现了一个长方体的线框模型,并实现了长方体模型的绕x轴，y轴，z轴的旋转.

关键词: 透视投影,线框模型

 

                          Knocking the door of  3D programming open

                             EmilMatthew([email protected])

Abstract: 

       By the implementation of rendening project method , realize a 3D rectangle model based on lines, also makes the 3D rectangle rotate around x axis, y axis and z axis.

Key Words: rendening project method, line model  

      

1前言:

       在计算机屏幕上去呈现出真实世界的3D的景象,需要对3D的图像经过一定的变换，使得在二维的介质上可以呈现出类似于三维世界的景象.显然，这是一个广阔,复杂而又激动人心的领域,涉及到投影，三维图形的实体表示，消隐面消除，真实感图形绘制，光照模型……本文所涉及的内容是该领域的入门级的内容，适合初学者(和我一样)借鉴.

       平面几何投影主要分为透视投影和平行投影，这里所谈的仅为透视投影，而且是透视投影中最简单的一点透视.

       所谓透视投影,便是计算机应用最多且普遍的一种投影模式。生活中也随处可见透视透影的例子：如画家画景物画，将画面布置的近大远小，以给人一种符合人们视觉效果的立体感受；再如照相机所拍出的照片等。所以，在计算机中实现透视投影，最能有效的表现出3D的立体的效果。

 

       2四元数及基本变换矩阵:

       注意:本文中所采用的坐标系为右手坐标系，所谓右手坐标系，即当拇指与某一坐标轴同时同向时，四指所指向的方向为绕该轴的正的旋转方向。（如图1）

                                  

                                                                图1

四元数可以用一维4元向量进行表达(如(x,y,z,1)T(T表示转置))，这里在x,y,z之外多出的一个维度值1，在与变换矩阵作基本运算时，起了很大的作用。可以用一个基本变换矩阵去表达某种变化方式（如平移，旋转），多个基本变换矩阵经过合理的组合，便可以表达一些比较复杂的效果.

       如平移的变换矩阵为:

                                              M1=                                   

       当点为P0= 时，其平移变换后的点，即为P’=P0*M1

再如绕    X,Y,Z轴的旋转变换矩阵为：

       绕X轴旋转:                             

       M2=                                  

      

      绕Y轴旋转:

      M3=

绕Z轴旋转:

M4=

       在对3D的领域进行深入学习时，四元数及变换矩阵将是一个非常基本的工具。但在本文中所涉及的内容，不使用四元数将会更简单，所以本文的实现没有用到四元数。

 

       3一点透视投影公式的推导:

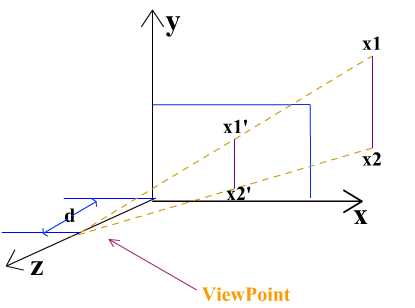
       如图2,对于实体对象，如果视点(Project Point)为(0,0,d),则真实对象直线L: x1x2在投影面xOy上的投影为x1’x2’(如图2)

          

                                                       图2

       可以根据相似三角形，对于任意x属于L，在L的投影面L’上的对应点为x’,

有:

                     d/(d+|z|)=x’/x

              =>  x’=d*x/(d-z)

=>  x’=x/(-z/d+1)        ……(1)

       对于任意y属于L，在L的投影面L’上的对应点为y’,同样有:

                     y’=y/(-z/d+1)         ……(2)

       这里一定要注意，照相机(Project)的距离一定要取得恰当,过远的话当无法看到三维效果。而取的过近，如d<=z时，将会出现类似在现实中照相机穿透到物体内部这种在现实中有可能成立但在计算机演示中绝不成立的效果。并且当d=z时，稍微健壮点的语言会立即抛出异常而导致程序运行中止。

       所以，通常取d=[2*|z|max,6*|z|max]为宜.

 

 

       4演示程序的结构:

       有了以上的理论基础，完成一个线框立方体绕x ,y ,z旋转的动画的最核心部分已经实现了.下面简要说明一下简示程序的结构以及线框模型数据结构的处理.这里采用Flash的AS2语言加以实现.

      

4.1立方体数据的保存:

       一个立方体一共8个顶点,12条线.

       动态显示时：可以采用”擦前次画线”à”画当前线”的简单步骤来进行

       线与线之前的关系可以用一个8*8的邻接矩阵来保阵，由于对称性，只取上三角邻接矩阵内的数据即可。

      

4.2演示流程:

演示流程如图3所示:

                                                        

                                                               图3

4.3关键代码:

采用面向对象的方式对结点对象进行封装:

import  E3DPack.*;

class E3DPack.E3DNode extends EObject

{

       public var x:Number;

       public var y:Number;

       public var z:Number;

      

       public function E3DNode(inX:Number,inY:Number,inZ:Number)

       {

              x=inX;

              y=inY;

              z=inZ;

       }

      

       public function resetXYZ(inX:Number,inY:Number,inZ:Number)

       {

              x=inX;

              y=inY;

              z=inZ;

       }

 

public function transTo2DNode2(projectPos:Number):E2DNode

       {

              var tmp2DNode:E2DNode=new E2DNode(undefined,undefined);

             

              var d:Number=projectPos;

              var r:Number=-1/d;

                           

              var newX:Number=x/(r*z+1);

              var newY:Number=y/(r*z+1);

      

              tmp2DNode.resetXY(newX,newY);           

              return tmp2DNode;

       }

      

       public function rotateAroundZ(fi:Number):Void

       {

              var tmpX:Number=x;

              var tmpY:Number=y;

             

              x=tmpX*Math.cos(fi)-tmpY*Math.sin(fi);

              y=tmpX*Math.sin(fi)+tmpY*Math.cos(fi);

       }

      

       public function rotateAroundX(fi:Number):Void

       {

              var tmpY:Number=y;

              var tmpZ:Number=z;

             

              z=tmpZ*Math.cos(fi)-tmpY*Math.sin(fi);

              y=tmpZ*Math.sin(fi)+tmpY*Math.cos(fi);

       }

      

       public function rotateAroundY(fi:Number):Void

       {

              var tmpX:Number=x;

              var tmpZ:Number=z;

             

              x=tmpX*Math.cos(fi)-tmpZ*Math.sin(fi);

              z=tmpX*Math.sin(fi)+tmpZ*Math.cos(fi);

       }

}

 

主调用过程:

function rotateTest():Void

{

       _root.gBrush.clear();//Pre frame clean.

       /*-------------Attention New brush make-------------*/

       _root.gBrush.lineStyle(1,0x6868FF,100);

       /*-------------End  of Attention-----------------------*/

      

       //rotation cacluating

       for(var i:Number=0;i<my3DNodes.length;i++)

              my3DNodes[i].rotateAroundZ(_root.gAngle);

       //showing

       drawCubic(_root.zProjectDis);

}

 

 

function drawCubic(projectPos:Number):Void

{

              if(projectPos==null||projectPos==undefined)

                     projectPos=1000;

                    

              for(var i:Number=0;i<8;i++)

                     for (var j:Number=0;j<8;j++)

                            if(connectMatrix[i][j]==1)

                                   {

                                                                                    my2DNode=my3DNodes[i].transTo2DNode2(projectPos);                                    _root.gBrush.moveTo(_root.gOffsetX+Number(my2DNode.x),_root.gOffsetY+Number(my2DNode.y));

      

my2DNode=my3DNodes[j].transTo2DNode2(projectPos);                             _root.gBrush.lineTo(_root.gOffsetX+Number(my2DNode.x),_root.gOffsetY+Number(my2DNode.y));

                                   }

}

4.4测试结果:

       a)程序正确实现了多边形绕x轴，y轴，z轴的旋转效果,具体效果及代码参附录.

       b)图4,图5分别呈现了在绕z轴旋转时投影点的距离不同所观察到的不同的物体的形变情况，可以看出，该程序正确反映出了透视图近大远小的效果.

    

                            图4                                 图5

 

       5实验结论:

       通过本程序，验证了理论的正确性，同时，也发现了书本中没有提及的实际问题，如d应取值大于|z|max等,可以以这个程序为基础，展开更多的3D效果测试。

 

参考文献: 

[1]倪明田,吴良芝,计算机图形学,北京大学出版社,2005.

                                                                                                         完成日: 05/01/22

 

附录:

1本文的Flash效果浏览:

绕x轴:

http://www.emilmatthew.zk.cn/EmilPapers/06_06Open3D/show/rotateX.html

绕y轴:

http://www.emilmatthew.zk.cn/EmilPapers/06_06Open3D/show/rotateY.html

绕z轴:

http://www.emilmatthew.zk.cn/EmilPapers/06_06Open3D/show/rotateZ.html

 

2本文最佳浏览定位:

http://www.emilmatthew.zk.cn/EmilPapers/06_06Open3D/index.htm

 

3测试程序下载:

http://emilmatthew.51.net/EmilPapers/06_06Open3D/code1.rar

 

4DOC文档下载:

http://emilmatthew.51.net/EmilPapers/06_06Open3D/doc.rar

若直接点击无法下载(或浏览)，请将下载(或浏览)的超链接粘接至浏览器地址栏后按回车.若不出意外，此时应能下载.