ACIS-Model Topology
Model Objects
An entity is the most basic ACIS object. It is implemented in the C++ class ENTITY. All entities have a common set of functionality, such as the ability to save and restore themselves to and from a file, copy themselves, and debug themselves. All other geometric and higher level ACIS model objects are derived from the ENTITY class.
A model object is any object that can be saved to and restored from a save file (.sat or .sab). ACIS model objects are implemented in C++ using a hierarchy of classes that are derived from the ENTITY class.
This chapter describes the ENTITY class and how the model geometry classes, model topology classes, and attribute classes (all derived from class ENTITY) are integrated together to form a model. For information about specific classes, refer to the reference templates in online help.
- The ENTITY Class
- Model Object Class Relationships
The ENTITY Class
The C++ class ENTITY provides basic model management functionality for all permanent objects in an ACIS model. The principle components of the model derived from ENTITY are topology, geometry, and attributes. Entities are always created on the heap and never on the stack. The C++ new and delete operators are redefined and overloaded.
All entities have a common set of functionality, such as the ability to be saved and restored to and from an ACIS save file, copy support, and debug support. This functionality is defined in two ways:
ENTITY
This class defines data and methods that all children of ENTITY inherit.
ENTITY_FUNCTIONS
This macro is included by all children of ENTITY, and provides a local instantiation (as opposed to inheritance) of much of the remaining functionality that is common to all model objects.
the ENTITY class itself does not represent objects within the modeler, any class that represents a permanent model object in ACIS must be derived from ENTITY in order to Inherit the common data and functionality that is mandatory in all permanent objects.
ACIS provides run-time mechanisms for identifying the type of any object derived from ENTITY, as well as its level of derivation. Refer to the 3D ACIS Application Development Manual for information about identifying model objects.
Figure 1 shows the derivation of some principal classes from ENTITY to illustrate the relationships. This diagram does not list all classes, nor even all classes in the principal components that are derived from ENTITY. All of the individual classes are described in detail in reference templates in online help.
Figure 1. Model Object Class Derivations
Model Topology
Topology refers to the spatial relationships between the various entities in a model. Topology describes how geometric entities are connected (connectivity). On its own, topology defines a "rubber" model, whose position is not fixed in space. For example, a circular edge and an elliptical edge are topologically equivalent (but not geometrically). Likewise, a square face and a rhomboid face are topologically equivalent (but not geometrically). A topological entity's position is fixed in space when it is associated with a geometric entity.
Topology can be bounded, unbounded, or semi-bounded, allowing for complete and incomplete bodies. A solid, for example, can have missing faces, and existing faces can have missing edges. Solids can have internal faces that divide the solid into cells. Bodies such as these are not physically realizable, but can be represented with ACIS.
ACIS separately represents the geometry (detailed shape) and the topology (connectivity) of objects. This concept is called boundary representation, or B-rep, modeling. This provides the ability to determine whether a position is inside, outside, or on the boundary of a volume (which distinguishes a solid modeler from surface or wireframe modelers). ACIS defines the boundary between solid material and empty space. This boundary is made from a closed set of surfaces.
- Topology and Boundary Representation
- Bodies
- Lumps
- Shells
- Subshells
- Faces
- Loops
- Wires
- Coedges
- Edges
- Vertices
Topology and Boundary Representation
The ACIS boundary representation (B-rep) of a model is a hierarchical decomposition of the model's topology:
Body
The highest level of model object, and is composed of lumps.
Lump
A 1D, 2D, or 3D set of points in space that is disjoint with all other lumps. It is bounded by shells.
Shell
A set of connected faces and wires, and can bound the outside of a solid or an internal void (hollow). Subshells form a further decomposition of shells for internal efficiency purposes.
Face
A connected portion of a surface bounded by a set of loops.
Loop
A connected series of coedges. Generally, loops are closed, having no actual start or end point.
Wire
A connected series of coedges that are not attached to a face.
Coedge
Represents the use of an edge by a face. It may also represent the use of an edge by a wire.
Edge
A curve bounded by vertices.
Figure 1 shows the relationship of the conceptual topology elements that define the boundary representation of an ACIS model.
Figure 1. Topology
These elements are implemented in ACIS using the C++ classes BODY, LUMP, SHELL, SUBSHELL, FACE, LOOP, WIRE, COEDGE, EDGE, and VERTEX. Each of these classes is derived from the ENTITY class. The specific data and methods of each class is described in the class reference template in online help.
The B–rep topology specifies the hierarchy of elements involved. For example, the topology of a hollow cube would include one body, one lump, two shells (one outside and one forming the inner void), 12 loops, 24 edges, and 16 vertices. It also specifies the relationships of these elements. For example, the inner void could be centered within the cube, or could be a small rectangular space off to one side. Within these relationships, transforms mathematically specify relative location, rotation, scaling, reflection, and shear.
Bodies(实心体)
Bodies are the highest level entities in ACIS models. Typically, a body is a single solid or sheet component, such as a washer, a stripped-down engine block, a zero thickness plate, or a cross section. A body can also be several disjoint bodies treated as one. A transformation recorded with the body relates the local coordinate system of the wires and lumps to the global coordinate space of the body.
(Bodies是ACIS数据模型中最高级别的实体,一个body可以是一个单个的solid实体(注意entity实体与solid实体(实心的体)的区别)也可以是一个(二维)薄面,如垫圈,拆开的发动机部件,无厚度薄板,或交叉的断面等都可看成一个body。几个不相交的body也可以看成一个Body.)
Bodies "own" any number of lumps: zero, one, or more. Figure 2 shows an example of a body with more than one lump. When a square block (solid lines) is cleared by a cylinder (dashed lines) whose diameter is slightly larger than the length of a side of the block, the block is separated into four lumps. Although the four lumps are not physically joined, they are still treated as a single body.
Lumps(区域)
A lump represents a bounded, connected region in space. A lump is an entire connected set of points, whether the set is 3D, 2D, 1D, or a combination of dimensions. Thus, a solid block with a dangling outside face is one lump, as is a solid block with an internal cavity. Two disconnected sheets are represented as two lumps.
(lump表示一个连接、有封闭边界的区域。一个lumps是一个连接的点集,不论这个点集是在3D、2D、1D还是一个混合空间中。因此,一个带有悬挂面或空腔的实体都作为一个lumps。两个不相连的薄面就是两个lumps.)
A body contains zero or more lumps, each of which represents a set of points that are disjoint from those represented by all other lumps in the body.
(一个Body包含0或多个lumps,每个lumps表示的点集合不相交。)
Figure 3 illustrates a body with two solid lumps. The large block represents one solid lump that completely encloses a void (dotted line). The second lump (small block with solid lines) is completely enclosed in the void.
{图3是一个包含有2个实体lumps的body。图所示的较大的块表示一个包含有一个封闭空间的实体lumps。第二个lumps是被包含在第一个实体lumps内部空间的用实线表示的小块。}
Figure 4 shows a body with a solid lump and a sheet lump. It is also possible to have solid and sheet regions within a single lump.
{图4显示包含一个实体lumps和一个(二维)薄片lumps的body。单个的lumps也可能包含有实体和薄片。}
Shells(外壳)
A shell is an entire connected set of faces and/or wires, including connections through a non-manifold vertex. Faces are connected together along common edges or at common vertices; wires may be connected to faces at end vertices.
A solid block with a dangling sheet is one shell, but a block with a cavity is two shells. A solid block with many embedded faces that are all connected through some path to the exterior faces is one shell, but a solid block with a disconnected "floating" embedded face is two shells (but one lump).
{一个shell是一个完全连通的面和线集,包括通过非流形顶点的连接。面顺着公共的边或公共的顶点连接在一起;线的端点被连接到面上。
一个带悬面的实心块是一个shell,但一个带空洞的实心块为两个shell(一个用于构成空洞的shell,一个用于构成外壳的shell).一个实心块带有内嵌面,这些内嵌面通过某些路径连接到外界面上,则该实心块就是一个shell,但是,如果一个实心块,内嵌在实体内的面是一个未连接的悬浮面,则该实心块就是2 个shell(但是一个lump)}
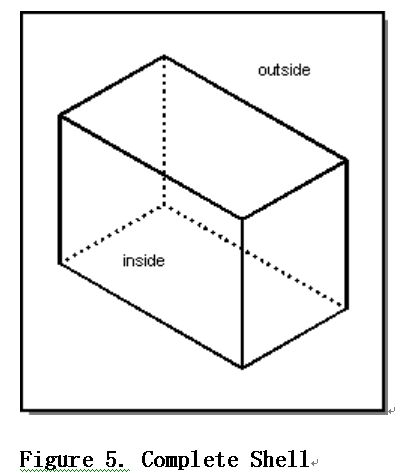
The most common type of shell is made up only of complete, finite single-sided faces (see section Faces), two of which meet at every edge, with compatible insides and outsides. Refer to Figure 5.
(最常见的shell 是通过边连接的一系列有限单面组成,每个面有一致的内部和外部属性,如图5所示)
(将shell可看成是相互连接的面和线构成,根据面的方向矢量,确定shell的所有面围成的区域是否构成一个有限的区域,这个有限区域就是一个三维实心的体)
Such a shell divides the whole of space into one finite region and one infinite one. If the finite region is inside the bounding faces, the shell is called peripheral, otherwise it represents a finite void in an object, and is called void. Refer to Figure 6.
{上面的shell将整个空间分为一个有限区域和一个无限区域。如果这有限区域在边界面的内部,则该shell就叫外壳。否则这个有限的区域就是物体内的一个有限的空洞,如图6所示}
If one or more edges have only one face attached, they are described as free edges, and the shell is open. If all the faces are double-sided and all exterior or all interior, then the shell is a double-sided sheet. If any or all of the faces are single-sided, or there are double-sided faces of both sorts, points in space cannot be classified unambiguously as inside or outside the shell, and it is described as incompletely-bounded, or just incomplete. Refer to Figure 7.
(如果一个或多个边仅仅在一个面上,该边称为自由边,所表示的shell就是开放的shell.如果所有的面是双边的,???,那么该shell就是双边的薄片。如果存在单边的面,或存在一个双边面,位于空间的点不能通过该面来明确判断该点是在shell的内部还是外部,说明该shell没有一个完全封闭的边界,如图7)
More than two faces may meet along an edge, in which case the edge is said to be non-manifold. Normally, if one collects together every face at a vertex that can be reached from a given face by crossing one or more edges starting or ending at the vertex, the collection contains all of the faces that meet at that vertex. If this is not the case, the vertex is said to be non-manifold. One or more wires may be attached to a vertex that is already on the boundary of one or more faces. This again makes the vertex non-manifold.
{两个以上的面共享一条边,这种情况下的边为“非流体”边。由多个面相交的一个顶点从该点沿着任何一个面的边移动,最后能回到该点。如果移动是跨越两个及两个以上的面,则该点为“非流体”点。(有关非流体,参看。。)}
A shell that contains any non-manifold edge or vertex is itself said to be non-manifold. For these more complex shells, the test for whether they are complete or incomplete is correspondingly more complex. Points in space close to single-sided faces are inside or outside according to which side of the face they are on. Points close to double-sided faces or wire edges are inside or outside, according to whether the face or wire is interior or exterior. Any other point is classified the same as another already classified point, if they can be joined by a continuous path which does not cross any face or wire. If every point in space can be classified unambiguously in this way, then the shell is complete; otherwise, it is incomplete. Any shell which contains a single-sided face with a free edge is automatically incomplete.
Bodies containing incomplete shells may only participate in modeling operations in regions where their shells are defined. Even then, some configurations give rise to ambiguous results, and so are disallowed.
Subshells
ACIS groups shells into a hierarchy of subshells for internal purposes. By computing and testing boxes that enclose subshells, ACIS can avoid accessing details of subshells and their descendent subshells and faces, which improves performance. Subshells are not accessible via the API, and are not generally used directly by applications.
Faces
A face is a portion of a single geometric surface in space, the two-dimensional analogue of the body.
Face Boundary Defined by Loops
Zero or more loops of edges constitute the boundary of a face. Figure 8 shows a loop of the top face (there are six faces) of a rectangular block.
Each loop determines a portion of the surface that is inside the face and a portion that is outside the face. If the face has no loops, the whole of the surface on which it lies is considered to be inside the face.
{每个loops确定表面的某部分是内面还是外面,如果其中一面没有环,则整个表面是内面}
If the inside and outside of all the loops are consistent (any line in the surface that joins a point inside to one outside must cross at least one loop) and the inside is connected, then the face is incompletely defined. A complete face whose inside is not bounded in space is said to be infinite. It is normally not meaningful to ask whether an incomplete face is finite or infinite. There are severe restrictions in ACIS on the operations that can be applied to infinite or incomplete faces.
{}
Face Sidedness, Sense, and Containment
A face's sidedness indicates whether it is single-sided or double-sided. A single-sided face has material (a solid region) on one side (the "inside"), and is void on the other (the "outside"). A single-sided face either completely or partially bounds a solid region, and the face divides the inside from the outside. (A single-sided face is a solid body, not a sheet body.) A double-sided face means that the points on either side are either all inside or all outside. If they are all outside, the face is considered to represent an idealized, infinitely thin sheet (a 2D region). If they are all inside, the face is an internal partition embedded in a solid.
The normal to a face can be either the same direction as the normal of the underlying surface at any position, or it can be the reverse of the surface normal. If it is the same as the surface normal, the face's sense relative to the surface normal is forward; otherwise, its sense is reversed. A single-sided face's normal always points away from the solid region (the material), regardless of the face's sense. Figure 9 shows a body with two single-sided faces bounding a solid region; the face normals point away from the material.
The following methods (member functions) of the FACE class are used to determine a face's sidedness, sense, and containment:
FACE::sides
- Face 1 is a spherical face that bounds a solid ball region; it is single-sided. The face normal points away from the sphere. The surface normal in this case also points away from the sphere, so the sense of the face is forward.
- Face 2 is embedded in a solid sphere; it is double-sided, both-inside.
- Face 3 is a 2D dangling flap; it is double-sided, both-outside.
Single-Sided Face Bodies versus Sheet Bodies
A single-sided face body is a solid body, not a sheet body. A sheet body is an infinitely thin body. ACIS considers a single-sided face body to be a solid that extends from the back side of the face out to infinity, with ill-defined boundaries extending where the edges of the original face extend backward. Because a single-sided face body is a solid, basic solid modeling concepts apply. Due to the ill-defined boundaries of a single-sided face body, subsequent solid modeling operations, such as Booleans, may not work, depending on how the single-sided face body is being used. When ACIS makes a body from a face, such as with API api_mk_by_faces, the body is a solid single-sided face, not a sheet body.
Loops
A loop represents a connected portion of the boundary of a face. It consists of a set of coedges linked in a doubly-linked chain which may be circular or open-ended.
If either end of an open-ended loop is at a finite point, then the face containing the loop is necessarily incomplete. If either end is at infinity, then the face is infinite.
The illustration in Figure 11 contains three closed loops. Each loop is the boundary of a complete, finite face. In the actual physical structure, the adjacent parallel lines are coincident.
Wires
A wire is a connected collection of edges that are not attached to faces and do not enclose any volume. Wires may represent abstract items like profiles, construction lines and center lines, or idealizations of rod or beam-like objects or internal passages. They are also commonly used to form wire frames to be surfaced to form solid-bounding shells.
A shell may contain a single wire or faces with multiple wires attached to them at vertices. A shell with just a wire is called a wire shell, a lump with only a wire shell is a wire lump, and a body with only wire lumps is a wire body.
Each wire is classified as being exterior representing an infinitesimally thin piece of material, or interior representing an infinitesimally thin passageway within bulk material.
Coedges
A coedge records the occurrence of an edge in a loop of a face. The introduction of coedges permits edges to occur in one, two or more faces, and so makes possible the modeling of sheets and solids (manifold or not). A loop refers to one coedge in the loop, from which pointers lead to the other coedges of the loop. Coedges in a loop are ordered in a continuous path around the loop and are doubly-linked. If a loop is not a circular list, the loop points to the first coedge.
In a manifold solid body shell, each edge is adjacent to exactly two faces; therefore, the edge has two coedges, each associated with a loop in one of the faces (the two faces can be the same, and even the loops can be the same). In this case, the two coedges always go in opposite directions along the edge. In a non-manifold body shell, there may be more than two coedges associated with an edge. In this case, they are ordered counterclockwise about the edge. Refer to section Edges below this section for more information.
In Figure 13, an isometric view of a solid shows three faces. Each face is bounded by a loop of coedges. Each edge (corner of the block) has two coedges, one for each face that is adjacent to the edge. Each coedge is coincidental with the edge adjacent and parallel to it.
Coedges in a loop are oriented so that looking along the coedge with the outward pointing face normal upwards, the face is on the left. In Figure 14, the directions of the face normals (blue arrows) and coedges (red arrows) for several faces of a body are shown to illustrate this orientation.
In a sheet body, there may be edges that have only one coedge. These are knows as free edges, and they mark the boundary of a sheet. If the face attached to the coedge is single-sided, the inside and outside of the associated shell are not well-defined near the edge, and so the shell is necessarily incomplete. (Refer to section Shells in this chapter for more information.)
Even though the edges of a wire meet no faces, each is given an associated coedge whose pointers link the edge to its neighbors.
The direction of a coedge can be either the same direction as its edge, or it can be the reverse of the edge direction. If it is the same as the edge direction, the coedge's sense relative to the edge direction is forward; otherwise, its sense is reversed. Each coedge contains a record of its sense relative to its edge.
Edges
An edge is the topology associated with a curve. The direction of an edge can be either the same direction as its underlying curve, or it can be the opposite direction. If it is the same as the curve direction, the edge's sense relative to the underlying curve is forward; otherwise, its sense is reversed. Each edge contains a record of its sense relative to its underlying curve.
An edge is bounded by one or more vertices, referring to one vertex at each end. If the reference at either or both ends is NULL, the edge is unbounded in that direction. If the underlying curve is infinite, so is the unbounded edge. When the curve is closed, the vertex references must both be the same or both NULL. If both vertex references are NULL, the edge is the whole curve; unless the curve is open and bounded, in which case the vertices must coincide with the curve ends.
A special case occurs when the geometry pointer is NULL and both vertex pointers point to the same vertex; for example, at the apex of a cone. Few ACIS operations work correctly with edges that have one or both end vertex pointers NULL.
An important feature of ACIS edge representation is the arrangement of the coedges around an edge. (Refer to section Coedges in this chapter for more information.) If only two faces meet at an edge, the two coedges from those faces point to each other through the coedge partner pointers. (If there is only one coedge, its partner pointer is NULL.) If more than two faces meet at an edge, the coedges are in a circular linked list. The order of the list is important, because it represents the radial ordering of the faces about the edge in a counterclockwise direction. Figure 15 shows a sheet body that contains a non-manifold (more than two faces incident) edge. The edge is directed such that it is coming toward the reader, and the coedges are ordered counterclockwise about it in the partner list as indicated by the arrow.
The purpose of radial coedge ordering becomes clear during traversal of an ACIS model that contains faces embedded with a solid region, such as in a 3D finite element model. Moving from a face across an edge to the radially closest adjacent face is a simple list operation, rather than a geometric operation as when coedges are not ordered. For example, moving to the face that is closest to the front (outward normal) side of a face is done by moving to the next partner pointer, if the original face coedge is FORWARD. If the original face coedge is REVERSED, moving to the closet face is done by moving to the previous partner pointer (obtained by walking all the way around the list).
In a non-manifold body shell, the edge may be adjacent to more than two faces. A non-manifold body is shown in Figure 16. An edge common to four faces is at each point where the cylinder is tangent to the outside edge of the block. In the example, edge ab is common to two faces on the inside wall of the cylinder (abcd and abfe) and two faces on the outside of the block (abgh and abjk). Edge ab is common to all four faces. When there are more than two coedges associated with an edge, they are ordered counterclockwise about the edge.
Vertices
A vertex is the corner of either a face (Figure 17) or a wire. Vertex refers to a point in object space and to the edges that it bounds. The other edges are found by following pointers through the coedges.