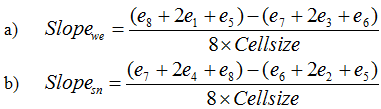GDAL使用DEM数据计算坡度坡向
零、 前言
之前写过一个3×3的通用模板算子函数的博客《基于GDAL的一个通用的3×3模板函数》,网址:http://blog.csdn.net/liminlu0314/article/details/8316156。当时说是要基于这个函数写一个计算坡度坡向的函数。由于这段时间一直忙于别的事情,这件事情就拖着了,今天给大家补上。
一、 简介
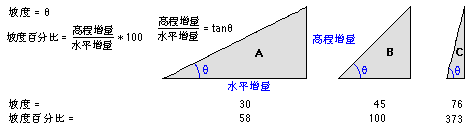
坡度(slope)是地表单元陡缓的程度,通常把坡面的垂直高度h和水平距离l的比叫做坡度(或叫做坡比)用字母i表示。【即坡角的正切值(可写作:i=tan坡角)】。坡度的表示方法有百分比法、度数法、密位法和分数法四种,其中以百分比法和度数法较为常用(如图1所示)。
图1 坡度的两种表示方法
1、百分比法
表示坡度最为常用的方法,即两点的高程差与其水平距离的百分比,其计算公式如下:
坡度 = (高程差/水平距离)x100%
使用百分比表示时,即:i=h/l×100%
例如:坡度3% 是指水平距离每100米,垂直方向上升(下降)3米;1%是指水平距离每100米,垂直方向上升(下降)1米。以次类推!
2、度数法
用度数来表示坡度,利用反三角函数计算而得,其公式如下:
tanα(坡度)= 高程差/水平距离
所以α(坡度)= arctan(高程差/水平距离)
如果将高程增量百分比视为高程增量除以水平增量后再乘以 100,就可以更好地理解高程增量百分比。请考虑下面的三角形 B。当角度为 45 度时,高程增量等于水平增量,所以高程增量百分比为 100%。如三角形 C 所示,当坡度角接近直角(90 度)时,高程增量百分比开始接近无穷大。
坡向(aspect) 是指地形坡面的朝向。坡向用于识别出从每个像元到其相邻像元方向上值的变化率最大的下坡方向。坡向可以被视为坡度方向。坡向是一个角度,将按照顺时针方向进行测量,角度范围介于 0(正东)到 360(仍是正东)之间,即完整的圆。不具有下坡方向的平坦区域将赋值为-1。如图2所示。
图2 坡向的取值
二、 坡度坡向计算方法
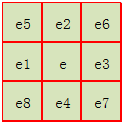
坡度计算一般采用拟合曲面法。拟合曲面一般采用二次曲面,即3×3的窗口,如图3所示。每个窗口的中心为一个高程点。图3中中心点e的坡度和坡向的计算公式如下:
上式中:Slope为坡度,Aspect为坡向,Slopewe为X方向的坡度,Slopesn为Y方向的坡度。
图3 一个3×3的窗口
关于Slopewe、Slopesn的计算可以采用一下几种常用的方法:
l 算法1
l 算法2
l 算法3
l 算法4
上式中的Cellsize为格网DEM的间隔长度。算法1的精度最高,计算效率也最高,其次是算法2。ERDAS Imagine中采用的是算法4,ArcMap采用的是算法2。本次也采用算法2进行实现。
三、 坡度坡向算法的编写
这里编写计算坡度和坡向的函数依赖于之前的博客《基于GDAL的一个通用的3×3模板函数》中的函数,所以这里只写出计算坡度和坡向的算法代码,具体调用参考博客《基于GDAL的一个通用的3×3模板函数》。通过博客《基于GDAL的一个通用的3×3模板函数》我们知道,要实现一个算法,需要写三部分的内容,分别是:算法参数的结构体;一个算法实现的回调函数和创建算法参数结构体指针的函数。
1、坡度
首先是定义坡度算法的结构体,计算坡度需要的参数有DEM格网的大小,也就是东西方向和南北方向的分辨率;高程的缩放比例;以及坡度的表示方式,即百分比还是度:
/**
* @brief 坡度算法数据结构体
*/
typedef struct
{
/*! 南北方向分辨率 */
double nsres;
/*! 东西方向分辨率 */
double ewres;
/*! 缩放比例 */
double scale;
/*! 坡度方式 */
int slopeFormat;
} GDALSlopeAlgData;
接下来是坡度算法的回调函数,该函数就是计算坡度的函数,按照上面的公式写就好,最后需要根据指定的坡度表达方式进行转换即可:
float GDALSlopeAlg (float* afWin, float fDstNoDataValue,void* pData)
{
const doubleradiansToDegrees = 180.0 / M_PI;
GDALSlopeAlgData*psData = (GDALSlopeAlgData*)pData;
double dx,dy, key;
dx =((afWin[0] + afWin[3] + afWin[3] + afWin[6]) -
(afWin[2]+ afWin[5] + afWin[5] + afWin[8])) / psData->ewres;
dy =((afWin[6] + afWin[7] + afWin[7] + afWin[8]) -
(afWin[0]+ afWin[1] + afWin[1] + afWin[2])) / psData->nsres;
key = (dx *dx + dy * dy);
if(psData->slopeFormat == 1)
return(float)(atan(sqrt(key) / (8*psData->scale)) * radiansToDegrees);
else
return(float)(100*(sqrt(key) / (8*psData->scale)));
}
最后是创建坡度结构体的函数:
void* GDALCreateSlopeData(double* adfGeoTransform, double scale, int slopeFormat)
{
GDALSlopeAlgData*pData =
(GDALSlopeAlgData*)CPLMalloc(sizeof(GDALSlopeAlgData));
pData->nsres= adfGeoTransform[5];
pData->ewres= adfGeoTransform[1];
pData->scale= scale;
pData->slopeFormat= slopeFormat;
return pData;
}
2、坡向
首先是定义坡向算法的结构体,坡向的参数很简单,就是一个是否使用方位角来表示,意思就是如果这个值设置为TRUE,坡度的计算结果按照图2中的角度进行表示,如果是FALSE,计算的结果是多少就是多少:
/**
* @brief 坡向算法数据结构体
*/
typedef struct
{
/*! 方位角 */
intbAngleAsAzimuth;
} GDALAspectAlgData;
接下来是坡向算法的回调函数,按照上面的公式写的,没啥难度。需要注意的是如果指定了bAngleAsAzimuth是TRUE的话,需要把计算的角度做一个转换,转换的结果就是0表示东,90表示北,180表示西,270表示南:
float GDALAspectAlg (float* afWin, float fDstNoDataValue,void* pData)
{
const doubledegreesToRadians = M_PI / 180.0;
GDALAspectAlgData*psData = (GDALAspectAlgData*)pData;
double dx,dy;
float aspect;
dx =((afWin[2] + afWin[5] + afWin[5] + afWin[8]) -
(afWin[0]+ afWin[3] + afWin[3] + afWin[6]));
dy =((afWin[6] + afWin[7] + afWin[7] + afWin[8]) -
(afWin[0]+ afWin[1] + afWin[1] + afWin[2]));
aspect =(float)(atan2(dy, -dx) / degreesToRadians);
if (dx == 0&& dy == 0)
{
/*Flat area */
aspect= fDstNoDataValue;//或者这里直接是-1
}
else if (psData->bAngleAsAzimuth )
{
if(aspect > 90.0)
aspect= 450.0f - aspect;
else
aspect= 90.0f - aspect;
}
else
{
if(aspect < 0)
aspect+= 360.0;
}
if (aspect ==360.0)
aspect= 0.0;
returnaspect;
}
最后是创建坡向结构体的函数:
void* GDALCreateAspectData(int bAngleAsAzimuth)
{
GDALAspectAlgData*pData =
(GDALAspectAlgData*)CPLMalloc(sizeof(GDALAspectAlgData));
pData->bAngleAsAzimuth= bAngleAsAzimuth;
return pData;
}
四、 结果展示
原始的DEM数据如图4所示,图5是计算的坡度值,图6是计算的坡向值。以下三个图像均是拉伸后的显示效果,由于DEM数据是16bit数据,计算的坡度和坡向数据是一个32位浮点型的数据。图像也没有进行分级渲染,用ArcMap处理的坡度和坡向数据做了一个彩色的渲染,效果比较好,当然这个就不再这里讨论了。
图4 澳洲新南威尔士州的一块DEM(SRTM数据)
图5 计算的坡度结果
图6 计算的坡向结果
五、 参考文献:
[1]Xiangling LIU, Glenn Otto (July 2013). The Determinants of Supply Elasticity in Sydney Housing Market,Working Paper,University of New South Wales
[2] http://help.arcgis.com/zh-cn/arcgisdesktop/10.0/help/index.html#//009z000000v2000000
[3] http://baike.baidu.com/view/1353583.htm
[4] http://help.arcgis.com/zh-cn/arcgisdesktop/10.0/help/index.html#//009z000000tr000000
[5] Burrough, P. A., and McDonell, R. A.,1998. Principles of Geographical Information Systems (OxfordUniversity Press, New York), 190 pp.
[6] http://baike.baidu.com/view/762866.htm