模式识别与机器学习基础之2---再看曲线拟合

声明：本文由英文原版“Pattern Recognition and Machine Learning”翻译而来，文中的插图均为原书的配图，只为学习目的。

在上文中已经知道了曲线拟合（polynomial curve fitting）问题可以用误差最小化（error minimization）概念来表示。这里用概率的观点来重新看待曲线拟合问题，因此对于以下概念要了解一下：error functions and regularization, as well as taking us towards a full Bayesian treatment。

曲线拟合问题的目的是，在训练集中得到N个输入x={x1,...,xn}T和其对应的目标值t=(t1,...,tn)T的条件下，给出一个新的输入变脸x得到目标值t。

可以使用目标变量的概率分布来表达不确定性。为了这个目标，假设，给出x的值，其对应的值t服从高斯分布（Gaussian distribution），这可以用y(x,w)表示的曲线公式表示。

现在训练数据{x,t}中，用最大似然值（maximum likelihood）来决定未知参数w和β。如果训练数据假定为独立分布(1.60)，那么似然函数可以用公式1.61表示：

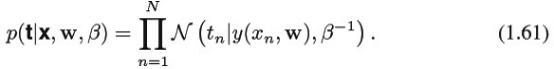
用替代形式的高斯分布，可以对似然函数变形如下：

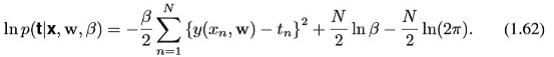
首先考虑多项式系数最大似然解，他是由参数WML决定的。这些都是有最大化w的值决定的。为了这个目的，可以可以省略去公式1.62右边的后两项，因为他们不依赖于w。此外，应该注意到通过正的常系数(positive constant coefficient)缩放（scaling）似然值并不会改变w的最大值的位置(the location)，因此可以把系数β/2替换成1/2。最后，不是最大化对数似然，我们可以等价的最小化负对数似然（the negative log likelihood）。因此，可以看到最大似然值是等价的，因此到目前为止应该关注的是确定w的值，从而最小化（公式1.2）the sum-of-squares error function。

我们可以通过最大似然值来决定服从高斯分布的参数β的准确值。最大化公式1.62的β值给出了公式1.63：

同样的，首先要决定参数平均的向量WML，随后利用这个来找出βML作为简单的高斯分布的确切值。

有了参数w和β以后，就可以对新的输入x进行预测了。通过一个概率模型，都是以预测分布（predictive distribution）的形式来表示t的概率分布，而不是简单的点估计。这是通过最大似然参数带入公式1.60得到：

现在，对于贝叶斯方法做进一步深入，通过多项式系数w来介绍一个先验分布（a prior distribution）。为了简单起见，考虑一个高斯分布的形式：

α是分布的精度，M+1是Mth阶多项式中向量w的总的元素数量。变量α控制了模型参数的分布，成为hyperparameters。利用贝叶斯理论，w的后验分布和先验分布结果成比例。似然函数为：

现在，可以通过在给定数据集下，检索最适合w的可能的值来决定w，话句话来说，最大化后验分布（the posterior distribution）。这种技术称为maximum posterior（MAP）。以公式1.66的负对数结合公式1.62,1.65，我们可以通过公式1.67的最小值来最大化后验值。

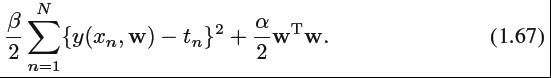
因此，可以明白了最大化后验分布和公式1.4中最小化正则的sum-of-squares error function是相同的，正则参数为λ=α/β。

附图公式1.4：